It is well known that the time derivative of the soft X-ray light curve for a solar flare is similar to the time profile of the impulsive hard X-ray emission for the flare. This is called the Neupert effect. It is less well known that the degree of consistence with the Neupert effect is different for different soft X-ray detectors. In particular, a detector with a response to radiation from high temperature plasma, such as the Yohkoh BCS, is much more likely to exhibit the Neupert effect than a wavelength band with a response to radiation from low temperature plasma, such as the Yohkoh SXT.
In this study, a simple correlation technique is used to determine whether the soft X-ray time derivative is similar to the hard X-ray light curve for each flare of a large sample of flares. In order to compare the degree of consistence with the Neupert effect at different temperatures, data from the FeXXV band of the Yohkoh BCS, and the Al.1 filter of the Yohkoh SXT are used in comparison with data from the Yohkoh HXT. The results are then compared to those obtained by comparing the soft X-ray curves to random samples of the hard X-ray curves.
For example, results for a sample of 267 flares show that high temperature radiation, as seen in the BCS-FeXXV channel, is consistent with the Neupert effect for 87 of the flares. This is approximately twice the number of flares that would show consistence from a random sample. For low temperature radiation, as seen by the SXT-Al.1 filter, only 18 of the 267 flares are consistent with the Neupert effect, which is slightly fewer than would be expected from a random sample.
It is well known that the soft X-ray time derivative is often similar to the hard X-ray (or microwave) light curve (Neupert 1968; Dennis & Zarro 1993). This is known as the ``Neupert effect''. It has been shown in theoretical work (e.g., Li, Emslie & Mariska 1993) that this effect can be reproduced if the flare energy release occurs in the form of nonthermal electrons. The nonthermal electrons lose their energy via Coulomb collisions in the lower corona and upper part of the chromosphere. The temperature rises and a high pressure region forms which drives material both upward and downward (chromospheric evaporation and chromospheric condensation). The coronal temperature and density are enhanced as the evaporated material rises, resulting in increased soft X-ray emission. The hard X-ray light curves are proportional to the time profile of the accelerated electrons. The soft X-ray emission, which is emitted from the plasma heated by the nonthermal electrons, is proportional to the accumulated energy deposited by the electrons up to a given time. The soft X-ray emission is thus proportional to the time integral of the profile of the input electrons (and the hard X-rays), and we therefore expect the Neupert effect. If we see the Neupert effect in the observed data, we can consider this to be evidence for chromospheric evaporation.
We would like to examine the Neupert effect as it applies to the behavior of plasma at different temperatures. In previous work with soft X-ray Differential Emission Measures (McTiernan, Fisher & Li 1999), we noted that the Neupert effect is more commonly associated with high temperature emission than with lower temperature emission. For this study we use the data from the Yohkoh BCS, SXT and HXT to discuss the Neupert effect in the low and high temperature ranges. The temperature responses of the SXT Al.1 filter and the BCS FeXXV channel are plotted in fig. 1. The SXT Al.1 filter is most sensitive to relatively low T emission, with a peak in the response at approximately 6 MK. The BCS FeXXV channel response has a broad peak near 50 MK, but since flare plasma temperatures do not generally reach such a high temperature, this channel is most sensitive to the plasma in the 20 to 30 MK range.
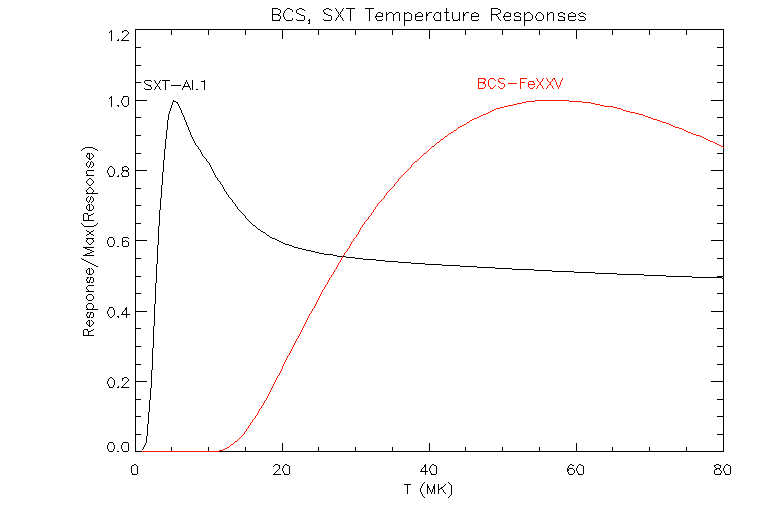
Figure 1: The normalized T response for the SXT Al.1 filter and BCS FeXXV channel used. The BCS responses are obtained using the IDL program BCS_SPEC, which is distributed as part of the SSW package. The solar coronal abundances used in the SW are adapted from Meyer, J.-P. 1985, Ap.J.Supp 57, 173.
Fig. 2 shows a comparison of the soft X-ray (SXR) count rate from the BCS FeXXV channel with 33-53 keV hard X-ray (HXR) data from the Yohkoh HXT, for a flare that occurred on 13-Jan-1992. The HXR data is plotted as a black line; the red line shows the SXR count rate, and the green line shows the time derivative of the SXR count rate. Here the SXR time derivative curve is very similar to the HXR curve; this is a clear example of the Neupert effect. In Fig. 3, the same comparison is shown using the SXT Al.1 data. The SXR time derivative looks nothing like the HXR curve; there is no Neupert effect.
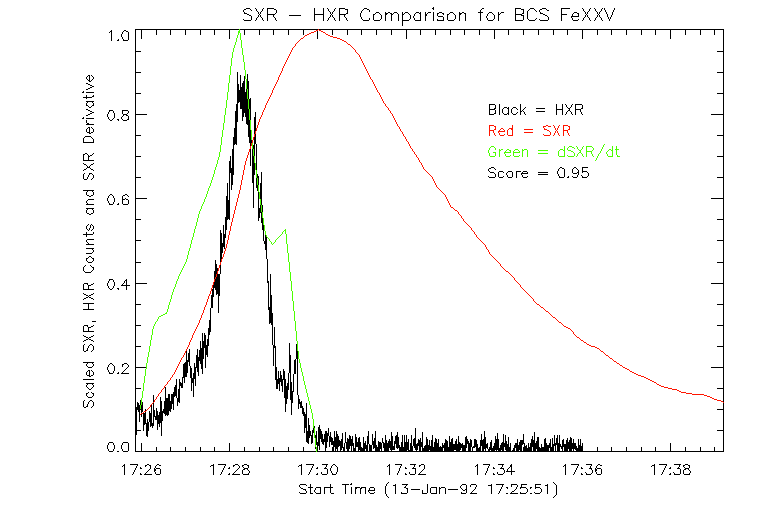
Figure 2: A comparison of the SXR count rate from the BCS FeXXV channel with 33-53 keV HXR data from the Yohkoh HXT, for a flare that occurred on 13-Jan-1992. The HXR data is plotted as a black line; the red line shows the SXR count rate, and the green line shows the time derivative of the SXR count rate.
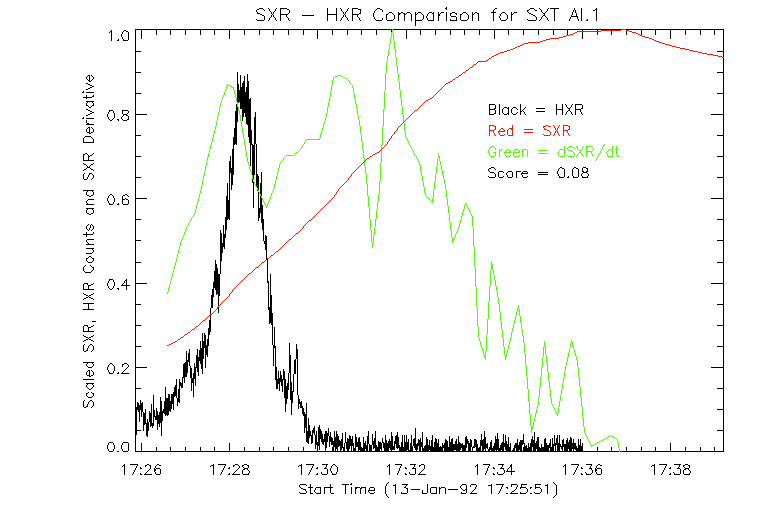
Figure 3: A comparison of the SXR count rate from the SXT Al.1 filter with 33-53 keV HXR data from the Yohkoh HXT, for a flare that occurred on 13-Jan-1992. The HXR data is plotted as a black line; the red line shows the SXR count rate, and the green line shows the time derivative of the SXR count rate.
We would like to find a numerical measure of the similarity between the SXR time derivative and the HXR curve. To accomplish this we do a simple correlation calculation; we define the Neupert ``score'' as follows:
The sign of the background-subtracted HXR count rate is compared with the sign of the SXR derivative. If the signs match for a given 9 second interval, then 1 is added to the score. If they do not match, then 1 is subtracted. The score is then divided by the number of intervals.
Score = ((no. matched signs) - (no. mismatched signs))/(total no. intervals)
The time intervals are determined by the SXR data, which for BCS has a time resolution of 9 seconds, and for SXT a variable time resolution of approximately 10 to 12 seconds. As seen in fig. 3, small fluctuations in the SXR data can cause large fluctuations in the SXR time derivative. To avoid this problem we simply assume that the SXR derivative is positive before the SXR peak, and negative thereafter.
The score ranges from -1.0 to 1.0 and flares with scores that approach 1.0 can be said to be consistent with the Neupert effect. For the BCS FeXXV data shown in fig. 2, the Neupert score is 0.95, an extremely high value. For the Al.1 data shown in fig. 3, the Neupert score is 0.08.
Note that a flare with no discernable HXR emission is assigned a score of -1.0.
We have applied this calculation to a sample of 267 Yohkoh flares from Oct-1991 to May-1998. The sample was chosen from the entire Yohkoh database for that time period, which contains approximately 1100 flares. Flares were rejected for a number of reasons: (1) For large flares the BCS, a very sensitive instrument, saturates, and no useful data is available. (2) In some cases there is a source seen by BCS, a full-Sun instrument, that is not present in the SXT data, since the SXT focuses on a given active region. (3) In other cases, there are different data gaps for the two different instruments which are too large for interpolation. (4) Flares which were too close to each other in time were rejected, since the SXR emission of flares is long-lasting (up to hours for some flares). (5) Flares for which the HXR peak was not observed were rejected; often flare-mode observations were not triggered until after the HXR peak. Any flare for which the HXR data in the first time interval was more than 0.8 times the peak HXR emission was rejected. (6) Flares for which there was less than 45 seconds of BCS data were rejected. Note that there is no restriction on the size of the flares in hard X-rays; this has not been true in previous studies (Dennis & Zarro 1993; McTiernan, Fisher & Li 1999).
For the sample of 267 flares for which we can make the Neupert effect comparison we find that for the high temperature BCS FeXXV data, there are 87 flares that have Neupert scores of greater than 0.80, and can be said to be consistent with the Neupert effect. To test whether this is a significant amount of correlation, we do the same comparison in a Monte Carlo calculation in which each soft X-ray light curve is compared with a random hard X-ray curve drawn from the same sample for a number of trials. (The exact procedure is discussed below.) From the random sample, for high T emission, we would expect 52(± 5) flares to have a score greater than 0.80, so the number of flares which show consistence with the Neupert effect in the original sample is greater than would arise from random chance, by approximately 7 sigma. This is shown in fig. 4, which is a histogram of the Neupert scores for the BCS FeXXV emission for the whole sample. The actual number of flares in each bin is shown by the black line and the expected number of flares is shown by the red line. It is obvious that there is a significant overabundance of flares with scores greater than 0.80. For low temperature SXT Al.1 radiation (fig. 5), only 18 of 267 flares have Neupert scores of greater than 0.80. From the random sample 25(± 4) would be expected to have a score of greater than 0.80. Thus the degree of correlation seen for low T is a bit less than that for a random sample, and is not significant.
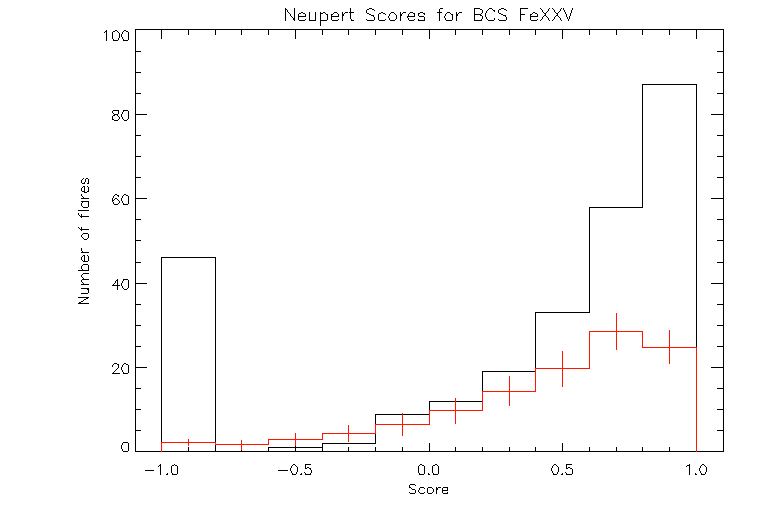
Figure 4: A histogram of the Neupert scores for the BCS FeXXV emission for the sample of 267 flares. The bin size is 0.2. The actual number of flares in each bin is shown by the black line. The expected number of flares is shown by the red line. The standard deviation of the expected number of flares is indicated by the error bars in each bin.
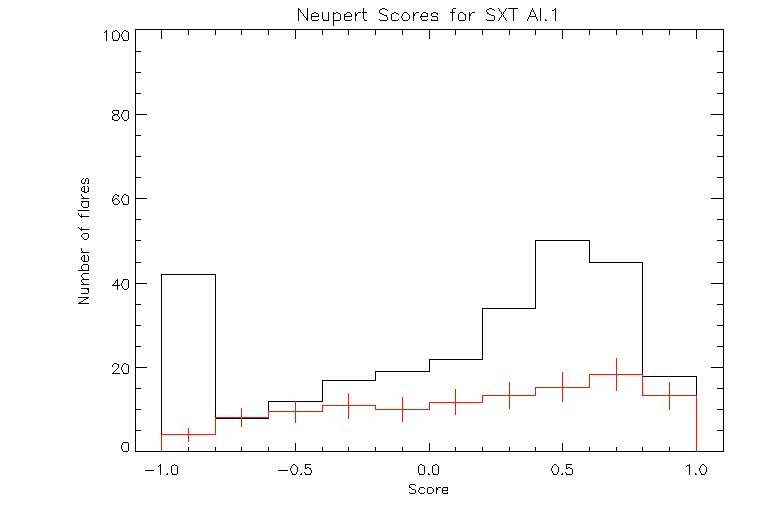
Figure 5: A histogram of the Neupert scores for the SXT Al.1 emission for the sample of 267 flares. The bin size is 0.2. The actual number of flares in each bin is shown by the black line. The expected number of flares is shown by the red line. The standard deviation of the expected number of flares is indicated by the error bars in each bin.
In order to test whether the amount of correlation that we find is significant, we compare each SXR flare to a random HXR flare drawn from the sample of flares (suggestion from U. Feldman) a number of times in a Monte Carlo calculation. The steps in this calculation are as follows:
(1) First the time profiles are scaled so that all SXR flares have the same duration. (Each HXR flare is scaled by the same amount as its SXR counterpart.) This means that we are only comparing the shape of the SXR and HXR profiles, not the duration.
(2) Next, the HXR flares are shuffled into a random order.
(3) The Neupert scores are calculated for the new SXR-HXR pairs, and the distribution of scores from -1 to 1 (in bins of 0.2) is calculated.
(4) Steps (2) and (3) are repeated 100 times (or sometimes 1000 times, the results are not affected), and the results are averaged. The uncertainty in each bin is given by the standard deviation of the 100 (or 1000) trials.
The results are plotted in Figs. 4 and 5
We conclude that the Neupert effect is a high T phenomenon. High temperature plasma, such as that observed by the Yohkoh BCS FeXXV channel, often shows the Neupert effect. Low temperature plasma, which dominates the radiation seen by the Yohkoh SXT, rarely shows this property. One cannot use this last fact to argue that the soft X-ray emission is not due to heating by energetic electrons, however. The low temperature plasma energy may be increasing later in the flare simply because high temperature plasma is cooling and becoming low temperature plasma itself.
In this study the percentage of flares which have been found to be consistent with the Neupert Effect at high T (approximately 33%) is much smaller than have been found in our earlier work (McTiernan, Fisher & Li 1999). This is why:
In the earlier study, only flares with large HXR count rates were used (> 100 counts/second in the M2 and HI channels of HXT, above 33 keV). Large flares tend to be more consistent with the Neupert Effect. In the full sample, for comparisons, emission from the M1 channel of HXT (23-33) was used for small flares. For whatever reason (most probably thermal emission contaminates the 23 keV channel) the lower energy HXR emission does not exhibit the Neupert Effect nearly as often. (In fact for low HXR energies, the HXR profile is often more similar to the actual SXR profile than to its derivative.) Also, many of the small flares in the full sample had no discernable HXT emission, so there could be no correlation for those flares.
In the earlier study any flare with a score greater than 0.60 was considered to be consistent with the Neupert Effect; here we are using a stricter standard by adopting 0.80 as the limit. If we restrict the sample to large HXR flares, and reduce the critical score to 0.60, then 73 of 115 flares (63%) are consistent, which is similar to the results of McTiernan, Fisher & Li (1999).
The author would like to acknowledge U. Feldman, A. G. Emsile and B. Dennis for suggestions and discussions. This work was supported by NASA grant NAGW-5126 and Lockheed subcontract LMSC-SA30G4740R.
Dennis, B.R. & Zarro, D.M. 1993, Solar Physics 146, 177
McTiernan, J.M., Fisher, G.H. & Li, P., Ap.J. 514, 472
Neupert, W.M. 1968, Ap.J. 153, L59
Preprints of McTiernan, Fisher & Li DEM paper:
Download from http://sprg.ssl.berkeley.edu/~jimm/dem98_pprx.ps