Anisotropy of RHESSI hard X-ray emission
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 74 |
| 1st Author: | Jana Kasparova |
| 2nd Author: | |
| Published: | 21 January 2008 |
| Next Nugget: | Solar Cycle 24 at hand! |
| Previous Nugget: | A STEREO/RHESSI Flare at Solar Minimum |
| List all | |
Contents |
Introduction
One of the most accepted models of particle acceleration and propagation during solar flares is the so-called thick-target model. This assumes that particles, e.g. electrons, propagating from an acceleration site in the corona towards the photosphere, are strongly downward beamed (although the beam must spread somewhat due for example to Coulomb collisions with ambient plasma and/or magnetic field convergence). If the electrons are relativistic, moving with a speed some reasonable fraction of the speed of light, the nature of the bremsstrahlung is such that X-ray photons emitted by the fast electrons are produced most probably along the direction of the electron's motion. Therefore, when the electron distribution is anisotropic, the photon emission should be anisotropic as well.
The study of emission anisotropy is thus very important, since it can tell us whether our "holy grail" model of the solar-flare impulsive phase is true, or whether we should seek something different or more realistic.
Albedo as a probe of anisotropy
Generally, the anisotropy of flare X-ray emission has been estimated either by simultaneous observations from at least two viewing angles (e.g. using well-separated spacecraft) or by means of statistical analyses of the distributions of spectral characteristics (such as photon flux and spectral indices) across the solar disc. It must be pointed out that such studies essentially measure the anisotropy only in the the upward hemisphere, i.e. towards the observer. However, there is another effect which can help us to study anisotropy. As was explained in [an earlier Nugget, the solar photosphere acts as a "dentist's mirror" and reflects originally downward X-ray photons back to an observer. This reflection by scattering, the so-called albedo, essentially gives us an independent look from below at the primary X-ray source.
Figure 1 in that Nugget shows an isotropic primary source above the solar photosphere. But what if the source is not isotropic? The amount of backscattered radiation is proportional to the downward-directed primary radiation. Thus the larger the downward anisotropy, the stronger the albedo component in the observed X-ray spectrum. The observed spectrum is then a combination of the primary emission directed towards an observer and the albedo component which is a distorted version of the downward-directed primary emission. Figure 1 illustrates this mixing of the components.
The method of Green's functions previously described allows us to separate these components and thereby to estimate the downward anisotropy in the vicinity of 20 keV. To simplify the problem, we describe the anisotropy of the primary source by a single parameter - the ratio of downward- to upward-directed photons.
First, we were successful in showing that the albedo component is indeed present in the X-ray flare spectra. We found that the distribution of the spectral index at about 20 keV significantly differs for the events located close to the disc centre (where the albedo contribution is large) compared with those near the limb (where the albedo component can be neglected). Moreover, the difference was removed when the spectra of the disc events were corrected for the albedo assuming isotropic primary emission - see Figure 2.
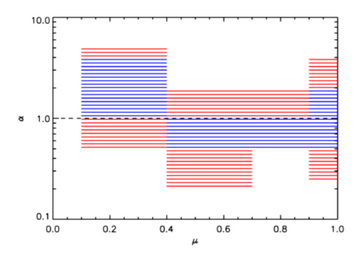
Secondly, by varying the anisotropy ratio, we were able to find ranges of anisotropy consistent with the data - see Figure 3.
Conclusions
The obtained range of anisotropy ratio and its large spread are consistent with isotropic primary emission (ratio equal to 1). The energy chosen for the analysis, 20 keV, is rather low and a large anisotropy is not expected even for a fairly strongly collimated beam. But we needed a large sample of events because our search for anisotropy is based on the statistical distribution against flare position. The chosen energy represents a trade-off between albedo characteristics and the requirement of a statistically significant dataset. Although no absolute conclusion about anisotropy at this energy can be made, the result lends support to other recent results suggesting quite isotropic electron distributions - are we witnessing a big challenge to the standard thick-target model?
Biographical note
Jana Kasparova is a postdoctoral researcher at the Astronomical Institute in Ondrejov, Czech Republic. This work was carried out in collaboration with Eduard Kontar and John Brown (University of Glasgow, UK).
| RHESSI Nugget Date | 21 January 2008 + |
| RHESSI Nugget First Author | Jana Kasparova + |
| RHESSI Nugget Index | 74 + |