Dips and Waves
From RHESSI Wiki
| Dips and Waves | |
|---|---|
| Number: | 115 |
| 1st Author: | Iain Hannah |
| 2nd Author: | Eduard Kontar |
| Published: | 23 November 2009 |
| Next Nugget: | A tiny white-light flare |
| Previous Nugget: | STEREO observations of flares and their associations with CMEs |
| List all | |
Introduction
Solar flares feature the acceleration of non-thermal particles of several descriptions. One of RHESSI's primary tasks is to study these particles via their bremsstrahlung X-rays. The X-ray spectrum typically follows a power law at high energies "hard X-rays", and an exponential at lower "soft X-ray" energies; in the standard interpretation these components reveal (respectively) the non-thermal energetic particles and hot plasma in the corona. The theory of the nonthermal x-ray radiation involves several processes: the initial acceleration of the particles, their propagation through the solar atmosphere, and their X-ray production as they lose energy to the background plasma. With several assumptions, can be wrapped up into a tractable problem in inverse theory. When this was first done at RHESSI's high spectral resolution, a new and unexpected feature tended to appear: a dip in the spectrum at about 30 keV.
There has been some heated discussion (for instance in this earlier Nugget) as to whether this "dip" seen in the mean electron spectrum derived from RHESSI X-ray observations is a real feature. It can often be removed by correcting for the albedo flux of X-rays scattered back to the observer from the solar atmosphere beneath the source. But for flares with relatively low thermal mission, the standard thick-target interpretation says that for an accelerated population of electrons above a low-energy cutoff the dip must be there. The thick-target model only accounts for Coulomb collisions between the propagating beam of accelerated electrons and the background plasma. In this Nugget we present simulation results from our recent paper, where we show what happens to the dip when you also include wave-particle interactions between the beam and the background plasma.
Wave-particle Interactions
In the standard interpretation of RHESSI's hard X-ray emission, a negative powerlaw of accelerated electrons (F0(E) ~E-δ for E>EC) above a sharp low energy cutoff leaves the corona travelling down to the chromosphere. As the electrons propagate they lose energy to the background plasma through Coloumb collisions, eventually stopping in the dense chromosphere, where they emit hard X-rays as observed by RHESSI. The collisional energy losses also heat the local plasma, which then expands back upwards along the magnetic field. It can be analytically shown the the resulting mean electron flux spectrum <nVF(E)> will also have a negative power law above the cutoff (<nVF>~E-(δ-2)) but will have a positive one (<nVF(E)>~E) below the cutoff energy. For flares with relatively low thermal emission the total mean electron distribution <nFV> will have a local minimum or "dip" between the thermal component and the positive slope of the low-energy non-thermal electrons.
We have simulated the propagation of such a power law of accelerated electrons, with only Coulomb collisions acting on the beam, as shown in the left panel of Figure 1. But we have also run a second set of numerical simulations in which we include the wave-particle interactions of the beam electrons and the background plasma. Specifically we include beam-driven Langmuir wave turbulence. We want to include the wave-particle interactions as this non-collisional process turns out to be faster than the Coulomb collision process. The development of Langmuir waves from electron beams in the solar atmosphere has long been inferred from radio observations of type III bursts, which are often associated with flares.
The use the weak turbulence approach describing the resonant interaction between the electrons and Langmuir waves. We follow in time the variation of the electron distribution function f(v,x,t) and, self-consistently, the spectral energy density of the waves W(v,x,t). In Figure 1 we show snapshots from the simulations showing f(v,x,t) for the Coulomb-collision simulation (left) and f(v,x,t) and W(v,x,t) for the wave-particle simulation (middle and right panel). A movie of this can also be found here.
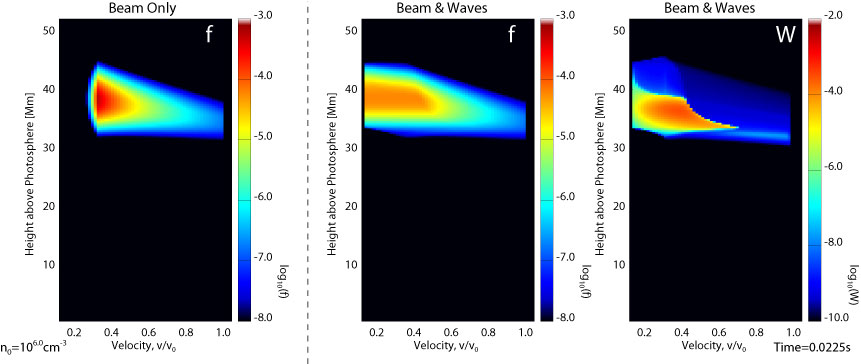
The immediate thing that happens is that the wave-particles very quickly flatten the low energy cutoff, producing a plateau in the electron distribution at low energies or velocities. The Coulomb collision alone are far slower at removing the low energy cutoff and produce the expected positive gradient in the electron distribution below the cutoff energy. To calculate the mean electron flux spectrum from our simulations we use the simulated f(v,x,t)/m, spatially integrating and averaging over time. The resulting spectra are shown in Figure 2.
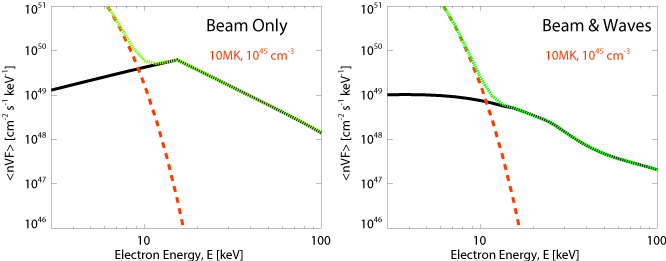
The positive slope increase in the Coulomb-collision-only case (left panel Figure 2) is clearly evident in the mean electron spectrum. The wave-particle interactions produce an almost flat, though slighlty negative, spectrum at low energies. With the inclusion of a thermal model spectrum, and using typical parameters for a small flare, we see the appearance of the local minimum or "dip" in the beam-only case. In the beam-and-waves case there is always a negative gradient.
Conclusions
The work shown here is a step towards a more complete treatment of electron transport in solar flares by consideration of wave-particle interactions. The inclusion of such effects goes beyond the traditional propagation theory, which typically relies on Coulomb scattering alone. The wave-particle interactions turn out to flatten any sharp low-energy cutoff in the inital accelerated electron distribution.
There are still other processes not included here, but this first look strongly suggests that the standard "thick-target" interpretation is insufficient to explain the RHESSI spectral observations and questions the suitability of a low-energy cutoff model for fitting RHESSI spectra.
| RHESSI Nugget Date | 23 November 2009 + |
| RHESSI Nugget First Author | Iain Hannah + |
| RHESSI Nugget Index | 115 + |
| RHESSI Nugget Second Author | Eduard Kontar + |