Is the coronal magnetic field braiding?
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 346 |
| 1st Author: | Markus Aschwanden |
| 2nd Author: | |
| Published: | 11 March 2019 |
| Next Nugget: | SOL2017-09-10 pulsations |
| Previous Nugget: | An energetic pre-flare: electron distributions in magnetic reconnection outflows |
| List all | |
Contents |
Introduction
How messy is the solar corona? The most beautiful high-resolution images we have seen from the Transition Region And Coronal Explorer (TRACE) and from the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO) exhibit paramount arcades of semi-circular loops, which are usually rooted near a sunspot in active regions, and have been interpreted as basically dipolar magnetic field configurations. In the simplest version, these loops appear like the field lines of a horse-shoe magnet, which confirms their dipolar nature.
Nugget
Sometimes, especially when solar flares become frequent in an active region, these bipolar loop arcades become twisted into sigmoids, as the Soft X-Ray Telescope on Yohkoh prominently displayed. This geometry of twisted sigmoids can be fittingly modeled by vertical currents above sunpots or other magnetic charge concentrations. Mathematically speaking, such helically twisted loops mimic divergence-free and force-free solutions for the geometry of the magnetic field, as it is expected from the MHD equations. We always were interested in such force-free solutions, because in the absence of forces, the field must be stationary and is therefore the most likely state in which a dynamical system is observed. Tacitly we assume that the geometry of coronal loops outlines the "true" coronal magnetic field.
So, after we have an explanation for helically twisted loops, we might play around with these field lines by twisting them more and more, perhaps up to several turns, to see if there are additional force-free solutions (see cartoons in Figure 2, which shows helical twists of zero, one, two, and three twisting turns. The celebrated Gauss had played around with such rubber bands, which can be twisted around each other as shown in the Figure. He tried to quantify these twists with a mathematical definition, and came up with a "linkage number" obtained by counting the number of windings (or helical turns). This is a part of the mathematics of topology with applications in molecular biology, DNA strands, material science, fluid mechanics, and astrophysics.
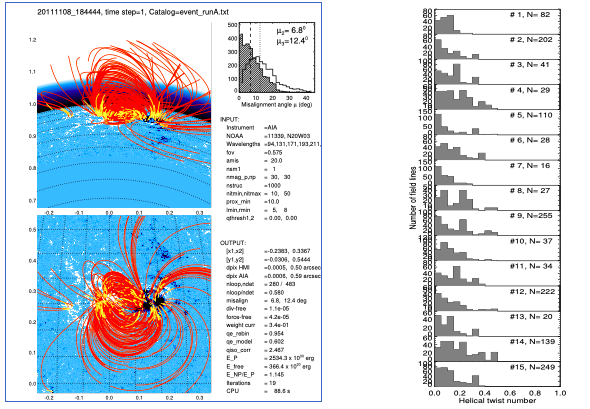
Here we are interested in measuring the linkage number of coronal loops. Fortunately, we now have a computational scheme (with the somewhat pathological name ``verical-current approximation nonlinear force-free field, VCA-NLFFF) code [1], that can fit force-free helical field lines to coronal loops as they are observed with AIA. A geometric definition of a helically twisted loop is depicted in Figure 1, and a typical fitting run with real data is shown in Figure 3, which shows a sigmoid with a twist of about a half turn. We measured this number of twists in 15 different active regions and always find that the number of helical twists is less than about a half turn (Figure 4). It is now widely accepted that coronal loops that are twisted more than a full turn become kink-unstable and erupt [2], which perfectly explains the absence of highly twisted (more than one full turn) flux tubes in a stationary active regions.
Conclusion
Why are we doing this topological exercise? Well, if the helical twisting exceeds one full turn (see Figure 2 with L = 1), or more (L = 2 or 3), we can describe this as a braiding topology of these intertwined loops. However, as Figure 4 shows, sigmoids are never twisted more than a half turn, and therefore, they are not actually braiding (Ref. [4]). This has far-reaching consequences, because many theoretical models of coronal heating assume that loops do necessarily braid in the corona [3], supposedly on unresolved spatial scales. Taking our new results of non-braiding coronal loops at face value, it appears that braiding does not occur in the corona. This does not exclude non-forcefree magnetic fields and braiding dynamics in the transition region and chromosphere, where the plasma beta parameter (i.e., the ratio of the thermal energy to the magnetic energy) can be smaller than unity, so that magnetic forces no longer dominate. This conclusion saves the theoretical nanoflare hypothesis originally proposed by Parker [4], if his nanoflares are placed down into the chromosphere or transition region, rather than in the force-free and non-braiding corona as originally proposed.
References
[2] "Ideal kink instability of a magnetic loop equilibrium"
[3] "Nanoflares and the solar X-ray corona"
[4] "Helical twisting number and braiding linkage number of solar coronal loops"
| RHESSI Nugget Date | 11 March 2019 + |
| RHESSI Nugget First Author | Markus Aschwanden + |
| RHESSI Nugget Index | 346 + |