Return currents and soft-hard-soft spectral evolution

From RHESSI Wiki

Introduction

In this Nugget we report the new approach to interpretation of hard X-ray emission in solar flares by considering both collisions and self-induced electric field created by the charge of precipitating electrons, or return current, presented in Ref. [1].

Hard X-ray emission in solar flares is often assigned to precipitation of beam electrons precipitating in Coulomb collisions from the corona into a flaring chromosphere, i.e. the "thick target" model. This precipitation can be traced from well-known variations of mean electron spectra (MES) with dips at lower energies and hard X-ray (HXR) spectra with double power-law HXR spectra. These are the classic HXR features of precipitating electron beams in solar flares:

1. The maxima of MES are shifted to higher energies up to 50 keV for more powerful softer electron beams (Ref.[2]).

2. Hard X-ray spectra in solar flares normally have a "broken power law," of the form A hν^-δ where δ changes abruptly at a specific "break energy." RHESSI now gives us high-resolution views of such spectra, showing spectral indices at lower energies (<70 KeV) being smaller by 1.5-3.0 powers than those at higher energies. The "break energy" at the elbow separating these spectral parts varies in a range of 30-60 keV; it is lower for harder beams and higher for softer ones.

3. Another striking property of these flare hard X-ray spectra in the impulsive phase is the nearly ubiquitous "soft-hard-soft" pattern of spectral evolution (e.g., Ref. [2]). In this pattern the softer spectra (larger δ) systematically occur at lower flux levels, so that the hard X-ray maxima have the hardest spectra (smallest δ) while the harder ones correspond to maxima in the hard X-ray emission. Such a pattern even appears in "footpoint" sources (Ref. [3]).

Electron beam kinetics in Coulomb collisions and Ohmic losses

Here we present additional kinetic treatment taking into account the effects not only Coulomb collisions but also an electric field induced by precipitating electron beams themselves. This theory makes use of the time-dependent Fokker-Plank equation in a flaring atmosphere with exponential variations of density and temperature.

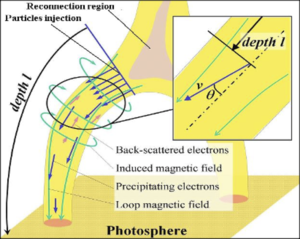
Let us assume a model in which electrons are injected at the top of a loop (see the cartoon in Figure 1) and "precipitate" downwards in the solar atmosphere. The number of precipitating electrons can vary from 10⁷ to 10⁹ cm^-3. While precipitating, these electrons constitute a current, and thus must create a significant self-induced electric field that, in turn, establishes a return current for compensation. The return current consists mainly of precipitating electrons, which changed their directions to upward motion during scattering on the ambient particles and of some part of the ambient electrons, which compensate the induced electric field. We compared stopping depths of precipitating electrons caused by collisions and losses in electric field showing that electrons with energies up to 80 keV become are dominated by electric energy losses for electric field induced by the beams with medium-to-high energy fluxes (see Table 1 in Ref. [1]). The outcomes of numerical simulations were also confirmed with the analytical solutions of a continuity equation for pure Coulomb energy losses.

By this means we have a full electric circuit of precipitating and returning electrons that keeps the whole system neutral, as Ampere's law requires, and supplies the required number of electrons per second. This resolving the electron "number problem" in a direct manner.

Figure 1: Cartoon showing model geometry.

Self-induced electric field and MES

The self-induced electric field E is associated with the number of precipitating electrons at a given depth that is dependent on the injected beam parameters as shown in the Figure 2, which shows the electric field variation with depth. Ref. [1] has compared stopping depths of precipitating electrons, with energies from 10 to 300 KeV, caused by pure collisions and by losses in electric field (see Table 1 in Ref [1]). This Table shown that electrons with energies up to 80 keV become more and more affected by electric energy losses if the beam's initial energy flux or a beam spectral index are increased (softer beams). In fact, the electrons below 80 keV lose much more energy to electric field losses than to the ordinary Coulomb collisions, the basic mechanism for stopping fast electrons in a plasma.

It can be seen that electric field losses can dominate collisional ones at very high levels in the corona at column depths of 10¹⁹cm^-2 (below the transition region of the flaring atmosphere), if the electric field is high enough. Since the pitch-angle diffusion of beam electrons in a presence of an electric field, actually, causes the preferential reflection of the lowest-energy electrons backwards because of scattering on the ambient particles, this contributes to the return current in itself. In fact, the return current at smaller precipitating depths is strongest, since there are only a few beam electrons yet scattered back, so that the the return current is dominated by the ambient electrons. At deeper precipitation depths there are more and more precipitating electrons scattered back by collisions, so that the return current becomes dominated by the returning beam electrons.

Figure 2: Variation of induced electric field with a precipitation depth, expressed as column density. The different lines show different spectral indices γ of beam electrons: 5 (solid line), 3 (dashed line).

The lower-energy electrons lose much more energy in the self-induced field and collisions than in the case of collisions only, and this results in their numbers being significantly reduced as is shown in the mean electron spectra (Figure 3). The more powerful and softer is the initial electron beam, the higher is a maximum in MES and the further it is shifted to higher electron energies.

Figure 3: Mean electron spectra distributions versus energy in keV for the two initial energy fluxes of electron beams 10¹⁰erg cm^-2s ^-1 (left) and 10¹²erg cm^-2s ^-1 (right) and the spectral indices &gamma: 3 (dot-dashed lines), 5 (dashed lines), and 7 (solid lines).

HXR photon spectra and SHS patterns

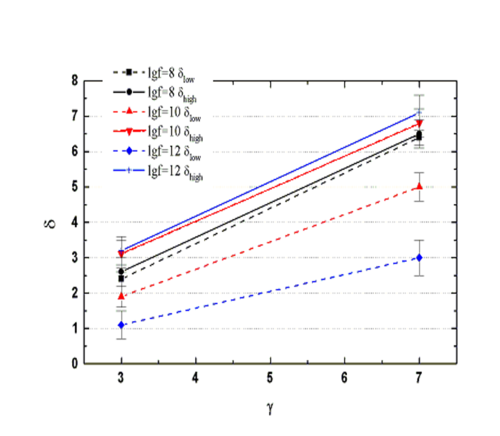
This effect of the self-induced electric field naturally leads to a harder X-ray photon spectrum at lower photon energies compared to higher photon energies, i.e. there is a flattening of HXR photon spectra at lower energies, while spectral indices at higher photon energies (> 40-80 keV) remain nearly the same. In Figure 4 the upper and lower spectral indices of HXR photon spectra are plotted versus different spectral indices of electron beams for different initial energy fluxes of the beams: upper indices (solid lines), lower indices (dashed lines). The higher the beam's initial energy flux F and its electron spectral index γ, the bigger is the difference between the spectral indices between the upper and lower spectral indices δ of HXR photons. This can naturally account for the origin of the broken power law of HXR photon spectra often observed in the photon spectra by RHESSI.

Figure 4: Variation of HXR photon spectral indices: lower (dashed lines), upper (solid lines) produced by electrons beams different energy fluxes. Note, the X axis shows the beam electron indices and Y-axis shows the photon indices.

Armed with this physics, Ref. [1] can explain the variations of the photon spectral index during solar flares, the so-called the "soft-hard-soft" (SHS) pattern described in other RHESSI Science Nuggets (cf., Ref. [2]).

At a flare onset, the initial beam fluxes are smaller, so are the self-induced electric fields induced by the injected electrons. As a result, the photon spectra have the single index close to what would be expected for a very weak beam, ie dominated by ordinary collisional interactions. At a flare maximum, the energy fluxes of electron beams are much stronger and induce much higher electric fields (see Figure 5). This leads to a strong flattening of their photon spectra as discussed above. After the flare maximum the beam fluxes decrease again, restoring the low-energy spectral slope.

Figure 5: Variations of HXR photon spectra for the initial energy fluxes of electron beams growing and dropping in time following a triangle profile; the red dot indicates the selected flux. It shows that at lower electron energy flux the photon spectrum has a single spectral index (S), then when the electron flux is increasing there is strong flattening (hardening) at lower photon energies, so the index is decreased (H) and when the electron flux becomes lower again the photon spectrum return to a single index again (S).

Therefore, because of the strong effect of deceleration of beam electrons by the self-induced electric field, this can explain the SHS patterns in photon spectra of flares. And this mechanism works not only in the footpoints of a flaring loop but also in the loop-top sources (Ref. [3]), where particles are accelerated if the loop-top region has a sufficient density to emit bremsstrahlung hard X-rays.

Please refer to the original paper (Ref. [1]) for full additional details.

References

[1] "The Effect of the Electric Field Induced by Precipitating Electron Beams on Hard X-Ray Photon and Mean Electron Spectra"

[2] "Spectral and Spatial Variations of Flare Hard X-ray Footpoints"

[3] "Electron Bremsstrahlung Hard X-Ray Spectra, Electron Distributions, and Energetics in the 2002 July 23 Solar Flare"