Peristaltic Shocks: a model
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 207 |
| 1st Author: | Dana Longcope |
| 2nd Author: | Roger Scott |
| Published: | September 16, 2013 |
| Next Nugget: | The Post-Burst Increase |
| Previous Nugget: | Negative Microwave Bursts |
| List all | |
Contents |
Background
In standard models of magnetic reconnection virtually all of the released energy remains on those field lines that have reconnected. The small amount of magnetic energy directly converted by the reconnection electric field is converted to heat or non-thermal particles which are both confined to field lines very effectively. Most of the energy release occurs later, through the retraction of field lines following reconnection (Ref. [1]). In Petschek's model this occurs within a steady outflow jet bounded by rotational discontinuities enclosing only reconnected field lines. This steady jet does little to transmit energy across field lines onto the unreconnected flux.
RHESSI's high time-cadence observations showing spectra and evolution of loop-top sources have frequently led investigators to conclude that non-thermal particle acceleration and propagation occurs in the presence of densities already enhanced by chromospheric evaporation (see, for example, earlier Nuggets). This conclusion is difficult to reconcile with the hypothesis that magnetic reconnection supplies the energy for both the evaporation and the particle acceleration. The energy release on a given field line can last only as long as its retraction. Retraction proceeds, according to all theories, at the Alfven speed, and thus much faster than evaporative flows. The energy release would thus end before evaporation could raise the density at the site of particle acceleration.
One possible resolution to this paradox would be a mechanism by which energy released by reconnection could be somehow transported across field lines onto the unreconnected flux. Such a mechanism would permit some evaporation in advance of the actual reconnection energy release on those field lines. This could also explain the high emission measure in the fan above a flaring arcade. In this scenario the fan would not correspond to the current sheet itself, but rather to a layer of pre-heated, and pre-loaded plasma surrounding the current sheet. It is through this layer that the remarkable supra-arcade downflows appear to descend, leaving behind them some form of trail or wake (Ref. [2]).
The Model
Our recent theoretical work (Ref. [3], the basis of this Nugget) has revealed a novel mechanism by which magnetic reconnection can transport energy onto unreconnected field lines surrounding the current sheet. In contrast to earlier treatments, this model simply assumes a patchy, unsteady reconnection process. The flux reconnected in a single patch forms a tube or bundle which retracts in a complex manner (not simply relating pairs of field lines) through the current sheet. The assembly of retracting flux tubes, formed from multiple retracting tubes, is the unsteady version of Petschek's steady outflow jet. Unlike the steady version, however, the retracting tubes will create moving deformations in the magnetized layer surrounding the current sheet. The response of the plasma to these moving deformations can lead to heating.
Figure 1 shows (in blue) a typical tube of unreconnected flux deformed by the presence of an intruding, retracting flux tube (black circle) moving though the current sheet (thicker red layer). The curve along the left edge shows the cross-sectional area of the blue tube. The maximum deformation, at the widest portion of the intrusion (z=0), reduces the area of the blue tube by nearly half. The curve along the bottom shows the maximum constriction for all the field lines in the unreconnected field. There is a layer about equal to the intruder's diameter where this constriction is significant; this is far thicker than the current sheet itself (red layer in the middle).
The downward motion of the intrusion creates a constriction in the surrounding tubes, which moves relative to the plasma at their far ends. (The action of the moving constriction resembles that in a peristaltic pump, so we refer to the flow as a peristaltic flow). The ends are assumed to be stationary while the constriction moves downward. The response to this moving constriction is similar to the response if flow had been driven from the far bottom through a stationary constriction: the classic de Laval nozzle problem. For downflow speeds of order the acoustic sound speed the flow is transonic at the narrowest portion as shown in Fig. 2. The condition necessary for transonic flow is achieved through a leading shock ahead of (below) the intrusion. This is a moving shock that propagates downward relative to the constriction. The flow then returns to the downstream state through a shock/rarefaction-wave combination, which propagates upward away from the constriction. These shocks in the peristaltic flow are termed "peristaltic shocks".

Observable structure
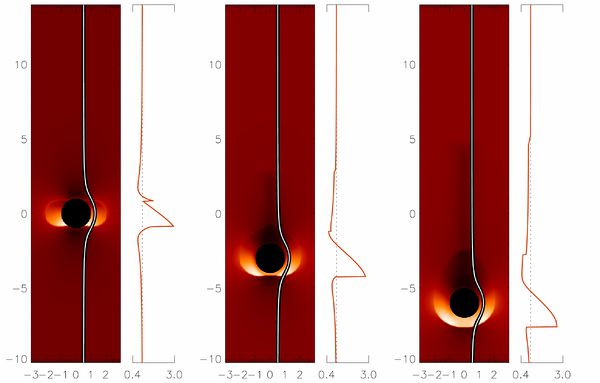
The result of the two shocks and single rarefaction wave in the unreconnected field may be seen in the evolving density structure shown in Fig. 3. A region of enhanced density builds up in front of the descending intrusion. A longer tail of reduced density persists in the wake of the intrusion. The red curve to the right of each panel, showing the density along that flux tube traced in white, exhibits abrupt jumps at the two peristaltic shocks and the rapidly receding rarefaction wave.
Shocks will heat the flux layer surrounding the current sheet, ultimately driving chromospheric evaporation there: the natural response of a coronal equilibrium subjected to additional heating. As subsequent flux tubes retract through the current sheet they will drive new shocks which will deposit more heat in the layer surrounding the current sheet. Eventually evaporation will raise its density to the point that it can radiate the additional heat deposited by repeated peristaltic shocks. This will form the layer of enhanced emission akin to those observed to surround actual current sheets. Moreover, when flux from this layer is eventually reconnected its pre-reconnection density will be higher than the ambient corona at a similar height. The energy conversion in this tube will occur in the presence of enhanced density. This novel scenario suggest a density enhancement that increases gradually as the flare progresses: early reconnection will occur on field lines which have not been subjected to peristaltic shocking.
Reinterpretation
For a perfectly circular intrusion shocks are produced by this mechanism only for descent speeds between 1 and 1.92 times the acoustic sound speed. This is significantly slower than the Alfven speed, so the surrounding field distortion is assumed to be current-free and to track the intrusion motion. The parallel flows driven by the moving distortion (i.e. the peristaltic flows) represent a kind of resonant non-linear coupling between fast magnetosoinc (FM) waves (the distortions) and slow magnetosonic (SM) modes (the flows and shocks). While FM waves cross field lines naturally, it is their resonant coupling that permits them to drive flows that shock and heat the plasma in the surrounding field. Thus heating by peristaltic shocking simply represents one possible fate for a fraction of the reconnection energy which is converted into fast magnetosonic waves. It is deposited in a thicker layer surrounding the reconnecting current sheet.
References
[2] "X-Ray Observations of Motions and Structure above a Solar Flare Arcade"
[3] "Peristaltic Pumping near Post-CME Supra-Arcade Current Sheets"
| RHESSI Nugget Date | 16 September 2013 + |
| RHESSI Nugget First Author | Dana Longcope + |
| RHESSI Nugget Index | 207 + |
| RHESSI Nugget Second Author | Roger Scott + |