Quasi-Periodic Pulsations: Fermi/GBM Results
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 161 |
| 1st Author: | David Gruber |
| 2nd Author: | Pawel Lachowicz |
| Published: | 24 October 2011 |
| Next Nugget: | Slowly but surely towards the huge amount of energy I |
| Previous Nugget: | Quasi-Periodic Pulsations: Fermi/GBM Results |
| List all | |
Contents |
Introduction
Over the past 40 years, quasi-periodic pulsations (QPP) in solar flares have been reported from observations across the electromagnetic spectrum on timescales from sub-second intervals up to several minutes. While there seems to be an overwhelming amount of observational data, the underlying physical mechanism that could generate such QPPs still remains unclear. There are several interesting physical explanations for pulsations, and there are broad implications elsewhere in astrophysics - for example, in the study of X-ray pulsars; see also one of our earliest RHESSI Science Nuggets.
In general, the analysis and interpretation of the power spectral density (PSD) of solar flares is difficult. This is because solar flares, together with many other astrophysical sources, have very steep power spectra in the low-frequency region. This type of variability is known as red-noise. When determining the significance of possible periodicities in the PSD, this red-noise component has to be accounted for in order not to severely overestimate the significance of identified frequencies.
Here, we present time series and periodogram analyses of four solar flares which were observed by the Fermi Gamma-Ray Burst Monitor (GBM) and display compelling quasi-periodic behavior in their light curves. A more comprehensive analysis on this subject can be found here, and a general review of coronal waves and oscillations here.
The Gamma-Ray Burst Monitor
The GBM is one of the instruments onboard the Fermi observatory, launched on June 11, 2008. Specifically designed for gamma-ray burst (GRB) studies, GBM observes the whole unocculted sky with a total of 12 thallium-activated sodium iodide (NaI(Tl)) scintillation detectors covering the energy range from 8 keV to 1 MeV, and two bismuth germanate scintillation detectors (BGO) sensitive to energies between 150 keV and 40 MeV. Therefore, GBM offers superb capabilities for the analyses of not only GRBs but solar flares as well.
What is red-noise?
Red-noise has nothing to do with measurement errors or the systematics (such as background counts) of the detectors, which are also called noise. Red-noise is an intrinsic property of the observed source and is due to erratic, aperiodic brightness changes. In contrast to white noise, which displays a flat spectrum in its spectral density. White noise is thus power that is independent of frequency, while red-noise is characterized by a power law of the form of P=N-α. This kind of variation is found not only in solar flares but also in e.g. X-ray binaries, Seyfert galaxies and gamma-ray bursts. As a first order approximation, red-noise is the realization of a linear stochastic and weakly non-stationary process.
In time-series analysis of solar flares, it is common practice to suppress this low-frequency component artificially by de-trending the light curves. This can be achieved for example by smoothing with a moving average or by applying a Gaussian filter and performing the periodogram analysis on the residual emission, i.e. the smoothed version is subtracted from the original data-set. Unfortunately, this procedure can give rise to misleading results as we show in the following.
By randomizing the phase as well as the amplitudes, one can generate a purely random time series that displays a 1/f&alpha: (red-noise) dependence in the spectral distribution. We created a time series with an f-1.8 periodogram shape, subtracted a simple moving average and then calculated a Lomb-Scargle diagram of the residuals. The result is remarkable. Although we started with a purely random, red-noise dominated time-series, we obtain a PSD with three frequencies whose power exceeds the 3σ confidence limit. This approach in signal processing clearly returns false-positive frequencies - noise masquerading as true oscillations.
Shown by the example above, we strongly discourage subtracting smoothed versions of raw light curves when looking for intrinsic frequencies in the red-noise dominated spectral distributions.
One way to estimate the significance of induced frequencies on top of an underlying red-noise continuum in a spectral distribution was put forward by Vaughan. In his approach, one simply converts the periodogram into log-space in both frequency and power density. For such a log-periodogram, one can then clearly identify the power-law component in the low-frequency range and a "cutoff" where white noise or another, additional noise component takes over. One can easily determine the power-law parameters by fitting a linear function to the low-frequency periodogram bins using the least squares method.
Results
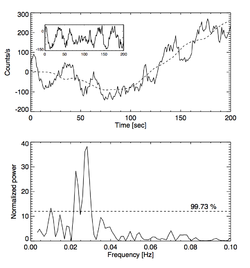
We calculated two periodograms of a RHESSI solar flare for which QPPs have been reported. Firstly, a Lomb-Scargle periodogram was calculated on the residual emission after a simple moving average was subtracted from the raw data. With this method, several peaks were found above the 3 σ threshold (see Fig. 2). The peak with the highest value of normalized power is located at f ~ 0.025 Hz. Another peak worth mentioning is located at f ~ 0.24 Hz, which is the expected rotational frequency of RHESSI around its spin axis and thus, an instrumental artifact.

As we now demonstrate, the significance of the peak at f ~ 0.025 Hz is highly overestimated by this method. In Fig. 2 an alternate spectral distribution is shown, calculated using the raw and undetrended light curve applying the technique introduced by Vaughan. A significant spectral feature at ~0.24 Hz is found which, once again, is the expected rotation period of the RHESSI instrument. However, this PSD is lacking any other frequency above the 3 σ confidence limit. The discrepancy between the two methods is easily explained. Firstly, the Vaughan method uses the whole raw light curve without artificially detrending it beforehand. Secondly, the method of Lomb and Scargle assumes a white-noise background continuum and does not take into consideration the red-noise component of the solar flare.
In conclusion, we did not confirm the reality of QPP in a RHESSI solar flare, as reported.
We then applied the aforementioned method to four solar flares which were observed by GBM.
All of these solar flares show a promising quasi-periodic behavior in their light curves, but none of these QPPs were statistically significant.
For clarity, only 2 out of 4 solar flares are shown here.
Please also see the
detailed analysis for further information.
Conclusions
Power spectra that are dominated by red-noise ensure that a periodogram analysis is not trivial, the interpretation of a peak in a PSD is more complex than usual, and that the estimate of the peak's significance is important. Again, red-noise is an intrinsic source property. In other words, having shown that the variations in the corresponding solar flares are not quasi-periodic at the 3σ level does not mean that these variations are not real.
While we consider it unnecessary to invoke oscillatory regimes of plasma instabilities, we note that the physics of these variations is certainly interesting and worth further study.
| RHESSI Nugget Date | 24 October 2011 + |
| RHESSI Nugget First Author | David Gruber + |
| RHESSI Nugget Index | 161 + |
| RHESSI Nugget Second Author | Pawel Lachowicz + |
