Free-bound continuum: basics
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 53 |
| 1st Author: | Brian Dennis |
| 2nd Author: | |
| Published: | 13 January 2007 |
| Next Nugget: | Thermal X-ray Continuum - Free-Free or Free-Bound? |
| Previous Nugget: | A myriad of microflares |
| List all | |
Contents |
Introduction
Solar X-ray astronomers have come to accept, almost without thinking, that the X-ray continuum emission from solar flares is bremsstrahlung produced by interactions of energetic electrons with atomic nuclei in the solar atmosphere. Bremsstrahlung is also known as "free-free" emission because the electrons remain free of the ions both before and after the interaction. In this RHESSI science nugget we explain how the physics of the X-ray continuum is much richer than this.
Another type of interaction called "free-bound" is possible between the electrons and ions, and it also produces an X-ray continuum. In this case, the initially free electron is captured by the ion into a bound orbit. It turns out that this type of free-bound interaction is much more likely for heavier elements than for hydrogen, with the cross-section depending on the fourth power of the number of protons in the nucleus of the ion (i.e. its atomic number Z). Thus, with the realization that the abundance of iron in the solar corona is some four times greater than it is in the photosphere, free-bound interactions become much more important and we can no longer assume that all the solar flare X-ray continuum emission is free-free bremsstrahlung.
Electron interactions in the solar atmosphere
The electrons accelerated to suprathermal energies (sometimes to well above an MeV) in solar flares are thought to lose most of their energy to the lower energy electrons present in the tenuous solar atmosphere through Coulomb interactions. These electron-electron collisions just involve the 1/r2 repulsive electrostatic force between the negative electrical charge on each electron. This is the way in which the flare energetic electrons heat the chromospheric plasma at the magnetic loop footpoints.
The energetic electrons also lose energy through interactions with the nuclei of the atoms in the solar atmosphere. These are mostly protons but nuclei of heavier elements up to iron and beyond are also present in small concentrations. Since electrons are much lighter than nuclei, they lose very little energy in Coulomb collisions with them compared to the energy they lose to other electrons. However, there are at least three other ways in which fast electrons interact with the nuclei. These are the free-free and free-bound interactions and the 'two-photon continuum,' all of which result in the emission of X-ray photons. (The latter does not contribute significantly to the measured solar flare X-ray flux above about 7 keV and is not considered further here.) The electrons lose only about 10-5 of their energy in these radiative 'nuclear' interactions. Nevertheless, it is these interactions that produce a big fraction of the X-rays that are seen with GOES and RHESSI. We understand the physics of these processes very well but there are still significant uncertainties in the various parameters needed to calculate their relative contributions.
Free-free radiation (bremsstrahlung)
In free-free interactions, illustrated in Figure 1, free electrons interact with the nuclei of the plasma and remain free after the interactions. The emitted photons are called bremsstrahlung from the German for 'braking radiation' since the electrons are 'braked': they lose energy in such interactions. Since opposite charges attract, you might expect that a negatively charged electron would be initially accelerated, and then equally decelerated as it swings past a positively charged nucleus. In fact, this is what usually happens, but in the classical picture, the acceleration bending the electron's orbit requires electromagnetic radiation to be emitted. In the quantum picture, this happens only probabilistically. In an unlucky collision The electron continues on past the nucleus but with reduced energy after emitting a photon. The energy of the emitted photon is just the amount by which the electron energy is reduced and so can be any value up to a maximum equal to the original electron kinetic energy.

Free-bound (recombination radiation)
A free electron can also become bound in a stable orbit around the nucleus and produce so-called 'free-bound' or recombination radiation. This is illustrated in Figure 2, where the electron is captured by the nucleus as the X-ray is produced and becomes bound in a stable orbit. The photon carries off the excess energy equal to the difference between the initial and final states of the system, i.e. always greater than the initial kinetic energy of the electron.
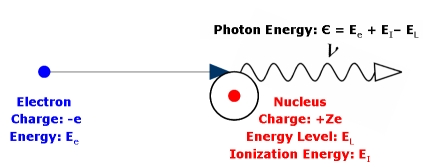
Free-Free & Free-Bound Spectra
The spectra of the photons that result from free-free and free-bound interactions are completely different, as illustrated in Figure 3 for the case of 30 keV electrons. The free-free spectrum is a continuum extending from the energy of the electron down to zero. The spectrum flattens with decreasing photon energy, reaching a power-law index of ~1.5 at 10 keV. In contrast, the free-bound spectrum covers a relatively narrow energy range above the electron kinetic energy. The difference arises because the photon energy from this free-bound interactions is the sum of the kinetic energy of the incident electron plus the binding energy of the state into which it recombines. The photon energy is greater than the electron kinetic energy, in contrast to the situation with free-free interactions where it must be less. The excess energy (the width of the blue box in Figure 3) is the energy level of the bound state. For fully ionized iron it can be over 7 keV.
A broad distribution of electron kinetic energies produces a continuum photon spectrum (the blue box in Figure 3 gets smeared out). It is important to note that a photon with an energy up to ~8 keV can be produced by an electron with zero kinetic energy if it becomes captured by a fully ionized iron nucleus. Thus, the free-bound continuum is very sensitive the electron spectrum down to very low energies. This is in contrast to the free-free mechanism, which isn't.
The probability of an electron being captured by a nucleus depends strongly on the charge (Z) of the nucleus and the resulting electric field that it produces. It turns out that this probability depends on Z4. Thus, an electron interacting with a bare iron nucleus has a factor of 264 = 5 x 105 greater probability of having a free-bound interaction than when interacting with a proton. Even with this large increase in the probability of free-bound interactions with iron nuclei, free-free interactions may dominate at hard X-ray energies with solar elemental abundances since protons are so much more abundant than iron nuclei - hydrogen is a factor of 105 more abundant than iron in the photosphere.
Conclusions
In a future nugget, we will explore the implications of the enhanced iron abundance in the corona on the relative contribution of free-bound radiation to the measured X-ray fluxes. It is now generally accepted that the iron abundance in the coronal relative to hydrogen is a factor of ~4 higher than in the photosphere. This can result in the free-bound flux exceeding the free-free flux, even in the hard X-ray regime. This has significant implications for relating the measured photon spectrum to the spectrum of the emittiing electrons since the standard equations are based on the assumption that all of the emission is from free-free interactions. Similar implications apply to the thermal emission from hot plasma, and this will be further explored using the CHIANTI modeling code and atomic data base.
Biographical note
Brian Dennis is a solar physicist at NASA's Goddard Space Flight Center, and is the RHESSI Mission Scientist and a CoI.
| RHESSI Nugget Date | 13 January 2007 + |
| RHESSI Nugget First Author | Brian Dennis + |
| RHESSI Nugget Index | 53 + |
