Harmonic Oscillations
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 132 |
| 1st Author: | Ivan Zimovets |
| 2nd Author: | Andrew Inglis |
| Published: | 2010 July 12 |
| Next Nugget: | Chromospheric Plasma Parameters |
| Previous Nugget: | Cloudy SolarSoftware |
| List all | |
Contents |
Introduction
Solar flare activity is often accompanied by quasi-periodic pulsations (QPP) in the flare emission, over a wide range of electromagnetic wavelengths. QPP carry important information about the processes occurring in flare regions and therefore are subjected to intensive scrutiny (see the [1] QPP events catalog]). Note that quasi-periodic oscillations in X-ray astronomy have similar mathematical properties, although often very different physics.
Covering a wide range of X-ray energy, the RHESSI satellite has great potential for deriving physical information from these variations. Two excellent examples of RHESSI observations exploiting QPP in solar flares have already been presented in the previous Nuggets 7 and 102.
However, one of the first rules of oscillation studies (and observations in general) is that you should always be on the lookout for potential instrumental effects – we must always consider the possibility that oscillations in our data are artificial rather than real. Time series of data can be subtly influenced by weak features that can be amplified by the analysis techniques applied to the data. In this Nugget we report on a striking instrumental effect peculiar to RHESSI, which leads to artificial (or rather, non-solar) oscillations of the RHESSI detector count rates during a powerful flare.
A striking example: the solar flare of 6 November 2004
Analysing the decay phase of the M9.3 class solar flare on November 6, 2004, extremely high-quality harmonic oscillations of RHESSI Corrected Count Rates in the 6-12 and 12-25 keV energy channels were surprisingly found. These oscillations have a characteristic period of 75 s and are clearly visible in the count-rate time profiles shown in Figure 1.
Pure harmonic oscillations of X-ray emission of such duration and quality are not typical for solar flares. Moreover, the X-ray detectors on board the GOES-10 satellite did not detect such a periodicity for this particular event. This leads us to consider two possibilities: the RHESSI observations are showing us (1) a rare solar flare phenomenon, newly discovered by RHESSI due to its sensitive detectors, or (2) an unexpected artifact present in the RHESSI data but not the GOES data.
Fortunately, the RHESSI telemetry contains the necessary information to resolve this dilemma.
RHESSI as a gyroscope
RHESSI rotates around its spin axis, pointed at the Sun, with a period of about 4 s. The bi-grid collimators mounted in front of each of the nine germanium detectors use this rotation to modulate the incident photon flux from solar flare X-ray sources on time scales much shorter than 4 s. Images can be reconstructed from the information in this rapid modulation (see "How does RHESSI make images?"). However, the imaging axis of the telescope is slightly offset from the spin axis so that it traces out circles on the Sun also with a period of about 4 s (see Nugget 57).
Since RHESSI is spinning freely in space, it behaves like a gyroscope, experiencing both precession and nutation. The precession and nutation produce motions of the telescope axis with respect to the X-ray source position. The time periods of the RHESSI precession and nutation are on the order of several minutes and several tens of seconds, respectively. The amplitudes and phases of these periodic gyroscopic motions change with time as RHESSI is subject to small external forces. The main force affecting these motions is from the Earth's magnetic field that is used through on-board magnetic torquer rods to both maintain the 15 rpm spin rate and to follow the Sun as it appears to move at ~1-degree per day with respect to the background stars.
The X-ray transmission through either one of the two grids that make up each bi-grid collimator falls off linearly as the source moves away from the direction normal to the grid, to give an almost triangular response curve with a minimum FWHM of about 1 degree. Thus, the average transmission through to the detectors is modulated as the angle between the direction to the source and the grid normal changes with time, both on the 4-s spin period but also on the longer precession and nutation periods. This, in turn, modulates the detector count rates and, we believe, produced the oscillations seen in Figure 1.
Not all of RHESSI's collimator grids have the same ~1-degree minimum field of view (FOV). Detectors 1 - 6 have grids with 1-degree FOVs but detectors 7, 8, and 9 have grids with FWHM FOVs of 4.4, 7.5, and 2.8 deg., respectively. This results in differing modulation amplitudes of the count rates for individual detectors - the larger the FOV, the smaller the modulation amplitude.
Let's return to the flare of 6 November 2004. In Figure 2(a) we plot the time profile of the angular distance (Delta, averaged over 4 s) between the RHESSI imaging axis and the flare position on the Sun. The figure also shows the corrected count rate (Normalized Amplitude) of RHESSI detector number 5 in the 6-12 keV energy channel during the time interval of the "pronounced" oscillations (see Figure 1). For visual purposes this count rate has been smoothed over 20-s, detrended, and then normalized by the maximum value.

It is clearly seen that the angle, delta, is anti-correlated with the Normalized Amplitude. Both oscillate with a period of about 75 s. (Note that delta also reveals the 4-s oscillations from the spacecraft rotation). This means that the greater the distance between the imaging axis and the flare position, the smaller is the detected X-ray flux. Despite the fact that the nominal 1-degree FOV of the RHESSI detector no. 5 is significantly larger than delta, a modulation of the count rates is still present. This is because the FOV follows a roughly triangular response curve with a FWHM of ~1 degree.
Although the normalization of Figure 2 suggests that the amplitudes in detectors 5 and 8 are similar, in reality the amplitude of the oscillations in the RHESSI detector count rates decreases significantly with increasing FOV of the corresponding grids, leading to the near-disappearance of the oscillations for detectors 7, 8, and 9.
These arguments demonstrate that the observed oscillations are a consequence of the RHESSI nutation. We confirmed this by plotting the lightcurves with RHESSI's OSPEX software, which corrects for the flare offset angle and the detector live time. This resulted satisfactorily in the disappearance of the oscillations in all detectors.
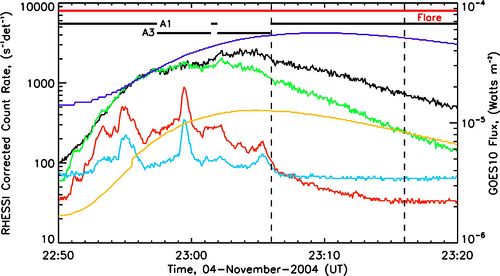
Antithesis of the 6 November flare: the "standard" flare of November 4
For comparison, we present analogous time series data of the M5.4 class flare from November 4, 2004, the decay phase of which behaved in the "standard" way without showing any obvious oscillations of the RHESSI count rates (Figure 3). This flare occurred in the same NOAA Active Region 10696 as the flare of November 6.
By comparing Figure 2 and Figure 4, it becomes evident that the amplitude of the oscillations of the RHESSI detectors count rates is inversely proportional to the amplitude of Delta oscillations. Relatively small modulations of Delta in the case of the 4 November flare do not lead to obvious oscillations of the RHESSI count rates.

Analysing several other solar flares, we came to the conclusion that the amplitude of the Delta oscillations (due to nutation) is not the only factor affecting the appearance of the oscillations of the RHESSI count rates and their character. But this problem requires further careful study and is beyond the scope of this Nugget.
Conclusion
Undoubtedly, RHESSI is an effective tool to study QPP of X-ray emission in solar flares, but its data should be used with care to avoid erroneous interpretations. This is because, by design, the imaging information RHESSI obtains is entirely encoded in the time series of the data, so that complicated modulations are inevitably present. If you find a periodicity of a few tens of seconds in RHESSI count rates, do the following steps to ensure that it is not the artifact described above:
1) Compare the oscillation period of the RHESSI count rates with that of the RHESSI imaging-axis oscillations due to nutation. This information is contained in the RHESSI aspect solution database. If there is a correlation, then be wary.
2) Make light curves for individual RHESSI detectors, say, detector no. 5 with a nominal FOV of 1 deg. and no. 8 with a FOV is 7.5 deg. If the modulation amplitude of the oscillations in detector 8 is smaller than in detector 5, then the oscillations can be considered suspect. Try plotting the lightcurves using OSPEX instead - this compensates for the detector response function.
3) Try to confirm the oscillations by analysis of relevant data from other independent instruments. This is the most effective way of ensuring oscillations are of solar origin!
Acknowledgements: We thank Valery Nakariakov, Aleksey Struminsky and Brian Dennis in particular for help.
| RHESSI Nugget Date | 12 July 2010 + |
| RHESSI Nugget First Author | Ivan Zimovets + |
| RHESSI Nugget Index | 132 + |
| RHESSI Nugget Second Author | Andrew Inglis + |