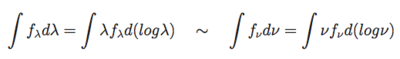Homing in on Flare Energy

From RHESSI Wiki

Introduction

We often want to represent the distribution of energy in the spectrum of an astronomical object, such as a solar flare. An energy spectrum can have many representations; two common ones are f_λ (in CGS, with wavelength units) ergs/cm² s A, or F_ν (in SI, with frequency units) W/m² s Hz. Needless to say, a profusion of other forms exists, often tailored to a specific kind of observation, and there is much nuisance involved in making comparisons. In flare physics this now has become very interesting, owing to the big breakthrough in Ref. [1], in which the total radiant energy of a solar flare could be determined bolometrically. Now the question is, where within the spectral energy distribution does a flare choose to put this energy? With modern broadband data such as those from SDO, we are now homing in on the answer to this long-standing question.

This Nugget explains a frequently-used stratagem for a quick visual overview of heterogeneous data. The basic trick is just to note that the energy, in whatever units, is the simple integral of the spectral energy (ie, per unit bandwidth). Thus f_λdλ and F_νdν both are simply energy or power, with suitable adjustments between the cgs and MKS (or other) representations. We realize that everybody understands this, and yet the Nuggeteers here have often confused themselves on this score, hence this Nugget. We plan to come back to this topic with further analysis in a future one.

Why λf_λ? Or νf_ν?

Because of Equation (1) here. This shows that if one plots this quantity on a linear-logarithmic basis, equal areas must have equal energies (or power levels, if the quantities are differential in time as well as bandpass). One can mix and match any spectral form here and obtain a correct representation.

This kind of representation is often used in non-solar astrophysics, where one may have skimpy data at wavelength (or frequency ranges) very distantly scattered across a spectrum many decades wide. An example appears here in Figure 1, taken from a page describing results at TeV energies that need to be compared with meter-wavelength radio data. This plot combines Nancay and H.E.S.S. data at the extremes, with other information in between.

A typical application of the νF_ν representation of the spectral energy distribution of an astronomical compact object (a BL Lac "blazar"). Note the twenty-decade breadth of the X-axis here, needed since H.E.S.S. observes at such high photon energies, and since this object has a large power content even at these highest energies. In this case the authors have chosen to compress the Y-axis logarithmically, which of course destroys the "area = energy" law for such plots, but adjusting for this is an easy mental exercise.

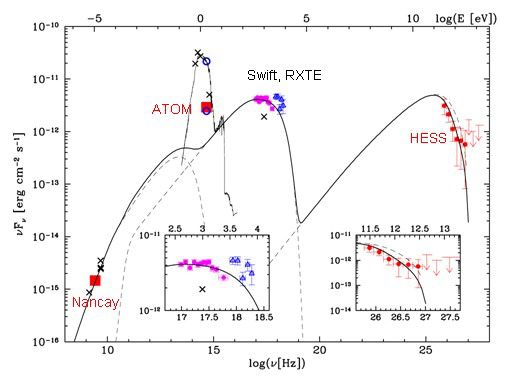
We do not often have to describe such greatly extended energy distributions in solar flares, but of course they do appear all across the wavelength range. for example, the thermal free-free spectrum seen by GOES and in thermal microwave emission underlies the whole spectrum from 1 A to 10 cm.

The case of the solar flare

A solar flare concentrates its radiant energy near the visible/UV range, but with much broader extensions at both extremes of the spectrum. The flare spectrum is broadband, but how much actual energy is in the extremes? The λf_λ plot shows us immediately, or at least points directly to our ignorance, and therefore should be taken seriously as a tool for planning future observations.

We present here some very preliminary views of the spectral energy distribution of the impulsive phase of the well-studied X-class flare SOL2011-02-15. These compare the white-light continuum from [Hinode/SOT] (Ref, [2]) and and spectral slices from SDO, as described below; in particular EVE shows a broad range of line and continuum emissions (Ref. [3]). The EVE range covers the Lyman continuum and some important transition-region lines in a continuous spectrum; at longer wavelengths we only have bits and pieces of data: the AIA UV passbands at 1600 and 1700 A.

Figure 3 shows λf_λ plots, both linear and log, with the available data. Clearly there is a major gap in our knowledge in the UV. We do not have systematic observations of the continuum in this range, nor do we have detailed line spectra that may in fact be dominant. Anecdotally, we do not think that the Balmer continuum (shortward of 3646 A) plays an important role, but that may change given the existence of active observational programs now searching for it.

Two representations of λf_λ for the impulsive phase of SOL2011-02-15. The upper plot is the true linear-log representation, for which equal areas imply equal energies; the lower plot shows the same data with a log compression on the Y axis. The dashed blue line is a blackbody at the temperature of the photosphere, fitted to the asterisks (red-green-blue measurements, in 4 A passbands, of the white-light continuum); the dotted line is the GOES free-free spectrum. The single point at about 4000 A is the H line, spread to 100 A width for plotting, and the three bands in the 1000-2000 range are the Lyman-alpha line and the integrated AIA 1600 and 1700 A fluxes.

The visual appearance of the energy distributions in Figure 3 is interesting. While the UV points look dominant, they are over narrow bands; the visible continuum (sketched here as a blackbody), though also not well observed, is broad and may contain the main energy. Until we get more complete UV observations we will not know directly.

Conclusions

This Nugget has no real conclusions, but does remind the solar community of the simple λf_λ (or νf_ν) representation of the energy distribution. The gaps in our knowledge are now much smaller than they were a few years ago, but they are important ones and need to be understood before we can be sure that we have properly understood the radiant energy of a solar flare. Right now it seems likely that solar flares have a lot of energy in the UV, perhaps more than in the white-light continuum, but we don't really know yet for sure.

References

[1] "Solar irradiance variability during the October 2003 solar storm period"

[2] "Physical Properties of White-light Sources in the 2011 February 15 Solar Flare"

[3] "Observations of Enhanced Extreme Ultraviolet Continua during an X-Class Solar Flare Using SDO/EVE"