The Jakimiec Track
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 96 |
| 1st Author: | Hugh Hudson |
| 2nd Author: | Fabio Reale |
| Published: | 2 March 2009 |
| Next Nugget: | High Temperatures in Active Regions |
| Previous Nugget: | Coronal implosion |
| List all | |
Contents |
Introduction
A great many tiny flares appear in the RHESSI data (and elsewhere). See the Nugget "A myriad of microflares" for an introduction, and stay tuned to the Nuggets pages for further interesting discoveries about them. The microflares (and the flares) occur in a power law distribution, which means that there is no well-defined average property (this is known "scale invariance"). The solar community (and many others) remain somewhat baffled by the deeper meaning of this fact, which is a bit difficult physically - normally one wants to have a clearly defined phenomenon to theorize about. That is difficult if there is no meaningful average. Another related concept is "stiction", a portmanteau word in the sense of Lewis Carroll. This one could be from "static friction" or maybe "sticking friction," but in any case its analog in the solar corona is Parker's nanoflare concept (Ref. 1). The idea of nanoflares is that an apparently steady X-ray emission could just be the result of innumerably many tiny, tiny non-thermal events (the nanoflares) that blend together imperceptibly. The connection with "stiction" is that something apparently smooth (thermal) actually consists of fine structure (non-thermal).
The (EM, T) diagram
We normally characterize the thermal spectrum of a microflare by its emission measure EM = n2V and its temperature T, because the X-ray flux S can be written as S = EM x f(T), where f(T) is a function of the temperature T that embodies most of the parameters that describe the emitting plasma and the specific detector that is making the observation. Here n and T are the plasma density and temperature respectively, and there are approximations involved in just saying this! Any good image of a solar flare shows it to be very complicated, so it is a gross simplification to imagine that it has these unique parameters; nevertheless to make progress in interpretation we often need to make this "isothermal" assumption. Of course for a stellar flare, or a very compact solar event, it is hard to see the complex structure, so that tends to ease the conscience a bit. Thus a plot of the two parameters (EM, T) naturally provides diagnostic information about the evolution of the flaring plasma. Many researchers have noted that the (EM, T) diagram for flares has interesting properties, and the claim has even been made that its organizing power may rival that of the Hertzsprung-Russell diagram- but for classes of flares, rather than classes of stars.
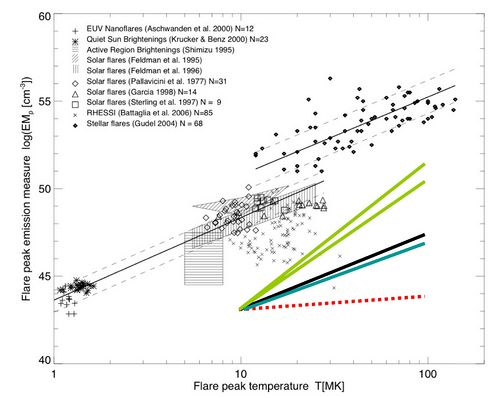
The diagram above shows clearly that the (EM, T) variables do have a strong organization. Here we are seeing one point per flare, but in principle one can observe the motion of that point as a function of the time as the flare evolves - hence the analogy, perhaps, with the Hertzsprung-Russell diagram. Here though we can watch the evolution on time scales of minutes, rather than Gy. The x's in this diagram show a sample of the RHESSI data analyzed by Marina Battaglia. The clouds of points may individually have correlations, as shown by the black lines, but different data sets seem to differ substantially. The RHESSI points in particular all look hotter (or with a smaller emission measure) than the bulk of the points in the original sample of Uri Feldman, which gave an excellent view of the correlation from the Yohkoh spacecraft. We go into the meaning of the brightly colored lines in the next section below.
The Jakimiec Track and scaling laws
To understand the distribution of points in the observational (EM, T) diagram, and their motions with time, we have in our mind a simple toy model (see Ref. 2). This consists of a coronal magnetic flux tube anchored in the chromosphere, which acts as a mass reservoir. The loop undergoes a heating process, finds an equilibrium possibly with continued energy input, and then decays. Because of the presence of the mass reservoir it has always been understood that radiative cooling dominates the ultimate decay of the energized loop since the radiative cooling rate is proportional to n2 . An under-dense loop can simply gain new gas from this reservoir, at the expense of a little conductive cooling, until radiation becomes important. If there is no further input as the loop cools down, it turns out that the emission measure n2V is simply proportional to T (n2V ~ T). This is shown as the dotted red line in the diagram, which we call the Jakimiec Track after J. Jakimiec, who discovered this relationship via numerical simulations done with the "Palermo-Harvard" modeling code of Peres and his collaborators. The blue-green line in the diagram shows the equilibrium series of the well-known "RTV" law. This law has n2V ~ T4.0. The black line has the same slope as the trend lines (also black) found by Aschwanden et al. simply to represent different groups of data; they have n2V ~ T4.5 approximately. The steep greenish lines show scaling laws derived by Shibata and Yokoyama from dimensional analysis of energy release with and without magnetic fields; these have n2V ~ T8 or so and don't seem to fit as well, but maybe they might if we were to think about the diagram in the right way.
Why do the greenish scaling laws not fit well, since they are based on such elementary principles in a toy model that really seems to match the observations viewed at their simplest level? Obviously one needs to be very careful with the observational material for various reasons. For example, different regions of the diagram have been observed with different instruments, with different and unavoidable biases. They thus may favor one temperature range over another; specifically the relatively narrowband EUV observations of EIT (or TRACE) strongly select in favor of ordinary coronal temperatures of 1-2 MK, rather than the hotter temperatures of flares. Another consideration is that a flare, as judged by the beautifully imaged solar ones, is not a single loop. Having different loops evolving with different time scales, both heating and cooling, will surely add model dependences that could confuse an interpretation in terms of a simple single-loop concept.
Conclusion
In spite of the profusion of data and the extensive modeling, which in fact can go far beyond the restrictions of the toy model, we don't have a clear understanding of flare occurrence, as seen in the (EM, T)-space of Figure 1 (the time distribution of flare occurrence would be a different matter). The data show without doubt that solar and stellar flares behave similarly (see an earlier Nugget) on this point. Are the "network flares" at the extreme left of this diagram also properly a part of this common pattern, or should they be adjusted along the Jakimiec Track to higher initial temperatures? Or do they represent some entirely new physics instead? Finally, is the agreement between the blue-green RTV law and the black empirical law merely fortuitous, given the instrument biases? Many questions remain unanswered!
References
0. Scaling Laws of Solar and Stellar Flares by M. Aschwanden et al.
1. Nanoflares and the solar X-ray corona by E. N. Parker
2. Diagnostics of stellar flares from X-ray observations: from the decay to the rise phase by F. Reale
3. A Hertzsprung-Russell-like Diagram for Solar/Stellar Flares and Corona: Emission Measure versus Temperature Diagram by K. Shibata and T. Yokoyama
| RHESSI Nugget Date | 2 March 2009 + |
| RHESSI Nugget First Author | Hugh Hudson + |
| RHESSI Nugget Index | 96 + |
| RHESSI Nugget Second Author | Fabio Reale + |