Chree Analysis for Flares
From RHESSI Wiki
(replaced ref. 3 with a more accessible one) |
|||
| Line 79: | Line 79: | ||
3. Kretzschmar, M. et al. (2010), ''The effect of flares on total solar irradiance'' [http://adsabs.harvard.edu/abs/2010NatPh...6..690K] | 3. Kretzschmar, M. et al. (2010), ''The effect of flares on total solar irradiance'' [http://adsabs.harvard.edu/abs/2010NatPh...6..690K] | ||
| - | [[ | + | [[Has article subject:: education]] |
Latest revision as of 02:26, 18 September 2018
| Nugget | |
|---|---|
| Number: | 98 |
| 1st Author: | Hugh Hudson |
| 2nd Author: | |
| Published: | 30 March 2009 |
| Next Nugget: | Cycle 24 - don't panic yet! |
| Previous Nugget: | High Temperatures in Active Regions |
| List all | |
Contents |
Introduction
"Chree analysis," named after Charles Chree, is now normally called "superposed epoch analysis." It is a powerful but tricky device, used effectively by Chree himself but often the source of erroneous conclusions. In this kind of analysis one takes a data series that contains interesting features, and then co-adds short segments of the series using some other source of information to provide a registration index. Thus if one could barely hear Big Ben chime from some distant location, one could just make a recording and then add up the parts centered on the hour as deduced from any other accurate clock. Eventually the noise would average down, and Big Ben's chimes would become strong enough to hear. That is the simple view. Although Chree himself used his method to make many important discoveries about geomagnetism (see Ref. 1), an unwary scientist can easily blunder using the technique.
Flare occurrence
Solar flares occur at odd intervals, but not randomly. There is an extensive literature discussing various aspects of this non-randomness, and Figure 1 (from a paper by Crosby et al.) illustrates one of them, namely the rigorous power-law pattern of flare magnitude. More energetic flares are less numerous, following the precise statistical relationship shown in the Figure. Below the weakest of these events one finds the microflares or even perhaps some of Parker's famous nanoflares.

The distribution function follows the power law N(E) = AE − γ, where A (the normalization of the number of events per unit time) and γ (the power-law index) are constants.
One interesting feature of this description (other than its amazing precision) is the flatness of the observed power law, i.e. the smallness of γ (it is 1.732 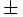 0.008; see Figure 1).
As any math student can show, the integral of this distribution diverges, i.e. it incorrectly "predicts" an infinite flare power since the integral of E.N(E) diverges if γ < 2.
This property is somewhat perplexing, since obviously the Sun does not shine by flares alone.
But it is not very perplexing because there should be some physical reason to truncate this distribution, and indeed this truncation may have been observed
already in an arcane piece of data: 12C in tree rings (dendrochronology), and fossil cosmic-ray tracks in the lunar regolith (Ref. 2)!
0.008; see Figure 1).
As any math student can show, the integral of this distribution diverges, i.e. it incorrectly "predicts" an infinite flare power since the integral of E.N(E) diverges if γ < 2.
This property is somewhat perplexing, since obviously the Sun does not shine by flares alone.
But it is not very perplexing because there should be some physical reason to truncate this distribution, and indeed this truncation may have been observed
already in an arcane piece of data: 12C in tree rings (dendrochronology), and fossil cosmic-ray tracks in the lunar regolith (Ref. 2)!
Signal or noise?
Given a well-defined occurrence distribution, how much does one improve the signal-to-noise ratio (SNR) by including a range of flare magnitudes? What we would like to do is to improve on the very important observation of flare effects on the total solar irradiance (Ref. 3), as shown for the single best example in Figure 2 below. The important thing to notice is the fluctuation (solar in origin) against which the flare effect must be detected. Can we add many time series of this type, guided by knowing the epochs of flare occurrence, to defeat this noise? The epoch in this case (the maximum, as marked by the arrow in Figure 2) coincides closely with the hard X-ray peak time as observable by RHESSI, although unfortunately not in this case.

Clearly one would benefit from a Chree analysis of (say) a set of flares all of the same magnitude.
Roughly the SNR would increase by about N1/2 as N increases.
But if one simply waits for flares to occur and takes them all, regardless of magnitude, would that help?
The answer turns out to depend on the value of the power-law index.
For a steep power law 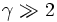 the actual value does not matter, and one gains the full N1/2 factor by including flares of all magnitudes.
But for a slope less than the critical value 2, it does matter.
Then it can be shown that the SNR grows much more slowly with magnitude range.
For R = Mmax/Mmin (R the ratio of the strongest and weakest events in the sample), we find that the SNR increases only as R2-γ, much more slowly than the increase in number of events.
The closer the power-law index comes to 2, the slower the gain via a Chree-type analysis.
the actual value does not matter, and one gains the full N1/2 factor by including flares of all magnitudes.
But for a slope less than the critical value 2, it does matter.
Then it can be shown that the SNR grows much more slowly with magnitude range.
For R = Mmax/Mmin (R the ratio of the strongest and weakest events in the sample), we find that the SNR increases only as R2-γ, much more slowly than the increase in number of events.
The closer the power-law index comes to 2, the slower the gain via a Chree-type analysis.
Conclusions
Even a simple-seeming and intuitively correct analysis technique can have tricky consequences. The Chree analysis does work in this case (see Ref. 3), but not as well as one would like. For a given SNR for the detection of a single X10-class flare, the extension to the M1 level (a factor of 100 in magnitude) would correspond to an increase in SNR of 3.6 (using the slope from Figure 1). While this is certainly not to be sneezed at - it might be just the factor needed to learn something really important about flare energetics - the weak dependence suggests that it is a difficult analysis.
References
1. Chapman, S. (1941), Charles Chree and his work on geomagnetism 1, 2, 3 (see especially part 2)
2. Reedy, R.C., Arnold, J.R., and Lal, D. (1983), Cosmic-ray record in solar system matter [1]
3. Kretzschmar, M. et al. (2010), The effect of flares on total solar irradiance [2]
education
| Has article subject | education + |
| RHESSI Nugget Date | 30 March 2009 + |
| RHESSI Nugget First Author | Hugh Hudson + |
| RHESSI Nugget Index | 98 + |