Imaging through visibility interpolation: uv-smooth
From RHESSI Wiki
| Line 50: | Line 50: | ||
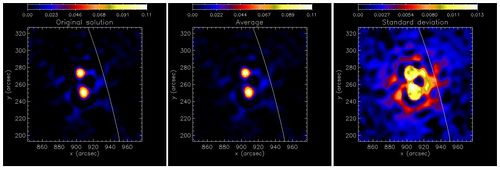
[[Image:Fig3_uv_smooth.jpg|500px|thumb|right|'''Figure 3''': 2002 February 20, 11:06:02-11:06:34 UT, event (energy range ε = 22 - 26 keV). Left panel: uv_smooth reconstruction. Middle and right panels: average of 100 uv_smooth reconstructions from randomly perturbed visibilities with the corresponding standard deviation.]] | [[Image:Fig3_uv_smooth.jpg|500px|thumb|right|'''Figure 3''': 2002 February 20, 11:06:02-11:06:34 UT, event (energy range ε = 22 - 26 keV). Left panel: uv_smooth reconstruction. Middle and right panels: average of 100 uv_smooth reconstructions from randomly perturbed visibilities with the corresponding standard deviation.]] | ||
| - | It is very easy to apply uv<sub>-</sub>smooth to real visibilities measured by RHESSI. You take the visibilities, interpolate them, apply the iterative algorithm and after a few iterations (the scheme typically converges in less than 20 steps) you have a nice image of the flare. Everything is fast, reliable and robust. A nice example is in Figure 3, which uses data from the 2002 February 20 | + | It is very easy to apply uv<sub>-</sub>smooth to real visibilities measured by RHESSI. You take the visibilities, interpolate them, apply the iterative algorithm and after a few iterations (the scheme typically converges in less than 20 steps) you have a nice image of the flare. Everything is fast, reliable and robust. A nice example is in Figure 3, which uses data from the [[Has event date::2002 February 20 11:06:02]] to 11:06:34 UT, event (energy range ε = 22 - 26 keV). In the left panel we show the uv<sub>-</sub>smooth reconstruction; in the middle and right panels we exploit the incredible speed of the method to perform a Monte Carlo experiment using 100 random realizations of the input data. The average image (center panel) and its standard deviation (right panel) are obtained in less than 30 seconds of computational time on a standard PC. |
== Conclusions == | == Conclusions == | ||
| Line 60: | Line 60: | ||
[1] [http://adsabs.harvard.edu/abs/2009ApJ...703.2004M Hard X-ray Imaging of Solar Flares using Interpolated Visibilities] | [1] [http://adsabs.harvard.edu/abs/2009ApJ...703.2004M Hard X-ray Imaging of Solar Flares using Interpolated Visibilities] | ||
| - | + | [[Has observation by:: RHESSI| ]] | |
| - | [[ | + | [[Has article subject:: education]] |
Latest revision as of 02:34, 18 September 2018
| Imaging through visibility interpolation: uv-smooth | |
|---|---|
| Number: | 113 |
| 1st Author: | Anna Massone and |
| 2nd Author: | Michele Piana |
| Published: | October 26, 2009 |
| Next Nugget: | STEREO observations of flares and their associations with CMEs |
| Previous Nugget: | |
| List all | |
Contents |
Introduction
RHESSI imaging works by image modulation, rather than by focusing. The raw data thus do not reveal the image immediately, but only after processing. This procedure is mathematically (but not physically) analogous to the manner in which an interferometic radio telescope images the sky.
Straightforward, traditional ways of making images from RHESSI data work much as you would use PhotoShop to enhance the image from a digital camera: you start with a "dirty map" of the flare and use deconvolution software (e.g., CLEAN, PIXON) to reduce the blurring effects of the collimators and so reconstruct a higher quality, less noisy, image of the real scene. This Nugget describes a recently-developed alternative approach, which is a little bit more sophisticated but which is tailored to the specific way in which RHESSI encodes imaging information. The rotation of the grid pairs of each of RHESSI’s Rotating Modulation Collimators (RMCs) provides a temporal modulation of the arriving flux; the pattern of this temporal modulation provides not so much an image but rather a specific set of spatial Fourier components of the source. These data, the purest form of the RHESSI data stream, are called visibilities – they are calibrated measurements of specific spatial Fourier components of the emitted radiation field. Visibilities are complex numbers with quantifiable (complex) error bars.
With its nine
RMCs, RHESSI produces visibilities on a set of nine concentric circles in the spatial frequency plane, each circle corresponding to the spatial frequencies sampled by a particular RMC as the spacecraft rotates. Because the grid pitches of RHESSI’s RMCs are arranged in a geometric progression with factor 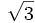 , the radii of these circles in the spatial frequency plane are also distributed in a geometric progression with the same factor; they range from 0.0027 arcsec-1 for the coarsest grids to 0.221 arcsec-1 for the finest grids. Armed with these visibilities, one can still reconstruct meaningful images by simply inverse Fourier transforming them from the frequency to the physical plane. However, such an approach, while at a first sight straightforward, is severely limited by RHESSI’s relatively sparse sampling of the frequency plane – there are simply not enough Fourier components available to make a high quality image.
, the radii of these circles in the spatial frequency plane are also distributed in a geometric progression with the same factor; they range from 0.0027 arcsec-1 for the coarsest grids to 0.221 arcsec-1 for the finest grids. Armed with these visibilities, one can still reconstruct meaningful images by simply inverse Fourier transforming them from the frequency to the physical plane. However, such an approach, while at a first sight straightforward, is severely limited by RHESSI’s relatively sparse sampling of the frequency plane – there are simply not enough Fourier components available to make a high quality image.
Enter uv-smooth. This new imaging technique uses a couple of simple but powerful mathematical tools to circumvent the problems of RHESSI’s sparse frequency-space sampling. The first of these is interpolation: uv-smooth generates a smooth continuum of visibilities within the disk encompassing the sampled area of the spatial frequency plane. The interpolation technique is a two-dimensional spline fit; it finds the locally minimally bent smooth surface passing through all experimentally sampled frequencies. (Think of a set of vertical tent poles on a set of nine circles in the ground [the measured visibilities]; uv-smooth finds the shape of the tent canvas that fits smoothly over these poles.) Once we have this continuous visibility surface, we can take the interpolated visibility values at regularly spaced points in the Cartesian spatial frequency plane and apply a very efficient
Fast Fourier Transform (FFT) technique to produce an image. Since this image is constructed from a relatively large number of Fourier components, it will be of considerably higher quality than the image produced using only the directly sampled visibility values.
The second crucial step in the method uses an iterative scheme that incorporates a positivity constraint - at each step the negative intensity values in the image (that are associated with ringing of each of the Fourier components) are removed and the Fourier transform of this modified image is taken. This new set of Fourier components is then smoothed as before and the corresponding image generated. As a result of this iteration scheme, additional Fourier components outside the sampled disk are generated. This effectively extrapolates the sampled RHESSI data set to higher spatial frequencies (i.e., smaller angular resolutions), so endowing the method with the property of super-resolution.
An illustration of the method
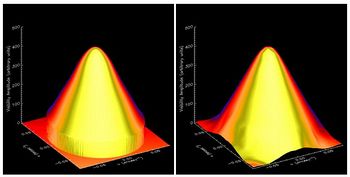
In the top left panel of Figure 1, the spikes (tent poles) you can see are the absolute values (magnitudes) of the (complex) visibilities that would be directly measured if RHESSI were to observe a simple two-dimensional Gaussian source. Processing these directly measured visibility values using an inverse Fourier transform results in a rather dirty, blurred reconstruction of the original Gaussian source (top right panel). Using uv-smooth, we replace the sparse (tent pole) data with a smooth continuum (canvas) obtained via spline interpolation: the measured visibilities are maintained while additional visibilities are added in between. The result is the surface of visibility magnitudes in the bottom left panel of Figure 1; a similar surface exists for the complex phase. This surface provides information inside the disk in the spatial frequency plane that is spanned by the measured visibilities, but with much more complete coverage. Computing the inverse Fourier transform of this smooth visibility surface using an FFT routine results in an image of the source; the iterative scheme discussed above is then applied to reduce the appearance of negative values in the image. The result is shown in the bottom right panel of Figure 1; the recovered image rather faithfully reproduces the form of the original source.
Note that the influence of the positivity constraint in the iterative algorithm that forms the second part of the method not only reduces ringing effects in the image but also has the rather magical consequence (justified by a beautiful and rigorous mathematical theory) that the visibility surface does not go to zero abruptly, as it does when using only data within the region of the spatial frequency plane sampled by RHESSI (left panel of Figure 2). Instead, as shown in the right panel of Figure 2, it drops to zero via a smooth tapering that effectively provides an extrapolation of the data in the spatial frequency plane and so (consistent with information theory) super-resolution in the image plane. This explains why uv-smooth is so accurate in reproducing the features (size, shape) of the original source.
A real flare
It is very easy to apply uv-smooth to real visibilities measured by RHESSI. You take the visibilities, interpolate them, apply the iterative algorithm and after a few iterations (the scheme typically converges in less than 20 steps) you have a nice image of the flare. Everything is fast, reliable and robust. A nice example is in Figure 3, which uses data from the 2002 February 20 11:06:02 to 11:06:34 UT, event (energy range ε = 22 - 26 keV). In the left panel we show the uv-smooth reconstruction; in the middle and right panels we exploit the incredible speed of the method to perform a Monte Carlo experiment using 100 random realizations of the input data. The average image (center panel) and its standard deviation (right panel) are obtained in less than 30 seconds of computational time on a standard PC.
Conclusions
uv-smooth is a very natural way for making images with RHESSI. It uses the RHESSI RMC data in its purest form, coupled with a fast FFT-based algorithm that makes image processing with uv-smooth extremely fast and reliable. Many experiments using simulated data have shown that it is applicable to a wide variety of source structures, reliably reproducing both the photometric intensity and shape of individual compact sources, and the intensity ratios of subsources within complex flaring structures. uv-smooth has been recently added to the RHESSI GUI. Try it! You won’t be disappointed.
Reference
[1] Hard X-ray Imaging of Solar Flares using Interpolated Visibilities
education
| Has article subject | education + |
| Has event date | 20 February 2002 11:06:02 + |
| Has observation by | RHESSI + |
| RHESSI Nugget Date | 26 October 2009 + |
| RHESSI Nugget First Author | Anna Massone and + |
| RHESSI Nugget Index | 113 + |
| RHESSI Nugget Second Author | Michele Piana + |