Understanding the co-spatial return current in solar flares
From RHESSI Wiki
m (→The return-current collisional thick-target model) |
|||
| Line 49: | Line 49: | ||
the following assumptions: | the following assumptions: | ||
| - | + | # Electrons are accelerated at the looptop with a single power-law spectrum and a sharp low-energy cutoff (E<sub>c). | |
| - | + | # The electrons lose some of their energy by return-current losses along the path toward the thick target. | |
| - | + | # They lose all of their remaining energy by Coulomb collisions. | |
| - | + | # We have a 1D model with electrons streaming along the loop and a co-spatial return current in the opposite direction. | |
| - | + | # The return current has had time to reach a steady state within the integration time of the spectra. | |
| - | + | # All the X-ray spectral flattening is due to return-current losses. This provides the upper limit of the return-current potential drop from the acceleration region to the footpoints. | |
| - | + | # Electrons are thermalized and lost from the beam when their energy reaches the lower limit of the cutoff energy. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | This provides the upper limit of the return-current potential drop from the acceleration region to the footpoints. | + | |
| - | + | ||
| - | + | ||
| - | + | ||
== Are the beam and the return current stable? == | == Are the beam and the return current stable? == | ||
Latest revision as of 02:17, 18 September 2018
| Nugget | |
|---|---|
| Number: | 330 |
| 1st Author: | Meriem Alaoui |
| 2nd Author: | Gordon Holman |
| Published: | 6 August 2018 |
| Next Nugget: | New Views of Global Solar Magnetic Field Evolution Over Four Solar Cycles |
| Previous Nugget: | 3D Magnetic Reconnection at a Coronal Null Point |
| List all | |
Contents |
Introduction
In the standard description of flare hard X-ray emission, an unspecified mechanism accelerates large numbers of electrons in the corona. These then penetrate into the lower atmosphere, creating "footpoint" sources of emission across the spectrum. These beams require return currents to balance the charge distribution. Co-spatial return currents have been proposed for this purpose. The return current locally neutralizes the charge build-up and cancels the magnetic field induced by the beam of accelerated electrons. Return currents solve the so-called number problem and the associated current stability problem. In this Nugget we describe the constraints on the flare-nonthermal electron distribution and its associated return current using RHESSI x-ray imaging-spectroscopy observations of many flares (Ref. [1]) .
The return-current collisional thick-target model
The flares studied in this work exhibit strong spectral flattenings of the x-ray spectrum at lower energies (a few deka-keV) during the HXR peak times. The magnitude of the flattening cannot be explained by mechanisms such as non-uniform ionization, isotropic Compton back-scattering, or pulse pile-up alone (see details in Ref. [1]).
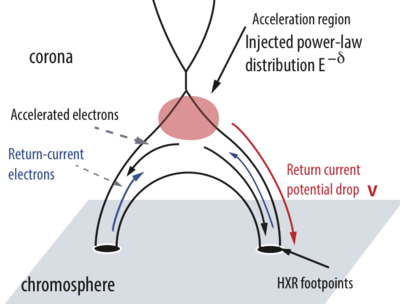
We consider a model (Figure 1) based on coronal magnetic loops, with the following assumptions:
- Electrons are accelerated at the looptop with a single power-law spectrum and a sharp low-energy cutoff (Ec).
- The electrons lose some of their energy by return-current losses along the path toward the thick target.
- They lose all of their remaining energy by Coulomb collisions.
- We have a 1D model with electrons streaming along the loop and a co-spatial return current in the opposite direction.
- The return current has had time to reach a steady state within the integration time of the spectra.
- All the X-ray spectral flattening is due to return-current losses. This provides the upper limit of the return-current potential drop from the acceleration region to the footpoints.
- Electrons are thermalized and lost from the beam when their energy reaches the lower limit of the cutoff energy.
Are the beam and the return current stable?
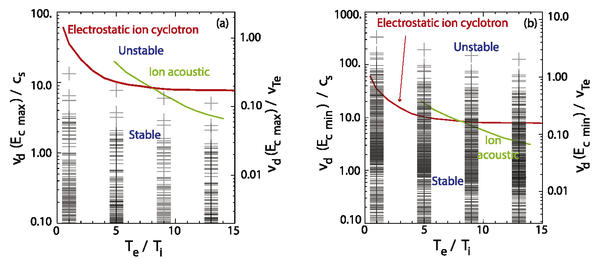
We have applied this model to a large number of flares, including some "early-impulsive" events (Ref. [2]) for which the non-thermal hard X-ray emission can be detected at lower energies, and others with clear flattening at low energies (the "spectral break") was clear. In each case we have evaluated the criterion for stability against the generation of electrostatic ion-cyclotron waves as well as ion acoustic waves and the Buneman instability, for which the threshold is about 2ve. For each case we can evaluate the drift velocity, assuming the beam current to be exactly balanced by the return current, and compare that with the known instability threshold (Figure 2). The comparison is made for separate estimates of upper and lower limits for the cutoff energy of the electron spectrum.
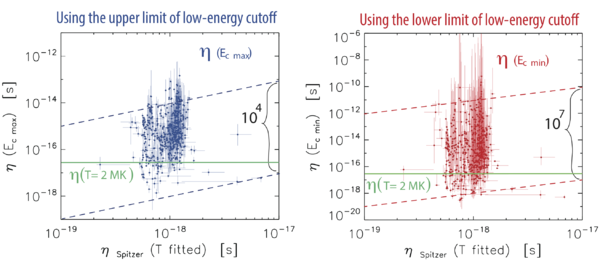
The resistivity is enhanced in most cases, if Ohm’s law is valid (figure 3). Current-driven instabilities are not the cause of that enhancement (figure 2). It is possible that the resistivity does not need to be enhanced, if part of the return current is carried by freely accelerated electrons. Ohm’s law is not valid then for calculating the resistivity, and the return-current electric field is on the order of the Dreicer field, which means runaway electrons cannot be neglected.
Conclusions
A main conclusion of the statistical analysis is that if the flattening is caused by return-current energy losses, then return currents are unlikely to be carried by only the bulk of the thermal distribution (electrons with velocities near the thermal speed, ve), but if the return current is carried by the bulk thermal electrons, the resistivity must be enhanced by a process different from the usual current-driven instabilities, namely, ion acoustic, electrostatic ion cyclotron, and Buneman instabilities. This was inferred from the result that the drift velocity of the return current was found to be lower than the threshold for generating these instabilities in all cases using the upper limit of the low-energy cutoff Ec, and in 506 out 528 cases using the lower limit of Ec.
Based on the results that these current-driven instabilities cannot explain the enhanced (anomalous) resistivity values, and that the return-current electric field is on the order of the Dreicer field, when the resistivity is classical, we will examine in an upcoming paper a scenario where the return-current carrying electrons are in the runaway regime, and whether the need for anomalous resistivity can be abandoned.
References
[2] "Nonthermal X-Ray Spectral Flattening toward Low Energies in Early Impulsive Flares"
| RHESSI Nugget Date | 6 August 2018 + |
| RHESSI Nugget First Author | Meriem Alaoui + |
| RHESSI Nugget Index | 330 + |
| RHESSI Nugget Second Author | Gordon Holman + |