This is an HTML version of my presentation at the SPD Meeting, at Bozeman MT. in June, 1997. If you're not familiar with the Yohkoh mission go to the YOHKOH SXT page at Lockheed, and read up. If you need to know more about Solar Flares, and X-ray observations, go to the NASA Solar Flare Theory pages.

THE VARIATION OF THE SOFT X-RAY DIFFERENTIAL EMISSION MEASURE VERSUS TEMPERATURE DURING SOLAR FLARES OBSERVED BY THE YOHKOH SXT AND BCS

J. M. McTiernan

Abstract

We study the behavior of the decay phase of solar flares using data from the Yohkoh SXT and BCS. In previous work, we have noted the difference in the slopes of the log(n)-log(T) plots for SXT and GOES. This led to an attempt to model the Differential Emission Measure (DEM) using those two instruments. We now add BCS data into the mix; instead of trying to fit the line profiles in the BCS channels directly we use the total line photon flux in each channel to find temperatures and emission measures. The loss of all information about the motion of the soft X-ray plasma is offset by the fact that we can now use BCS in the same manner as the broad-band detectors, to obtain information about the DEM. We have used parameterized model fits to the DEM, along with multi-temperature models, and Maximum Entropy Method (MEM) fits to estimate the dependence of the plasma cooling time as a function of temperature. Our results show that the flare plasma is not isothermal, and it is often difficult to describe the DEM using a smoothly decreasing function; functions of temperature with multiple peaks are often more useful. Using any kind of model, we find that higher temperature plasma peaks earlier and cools faster.

I. Background

We would like to study the behavior of the Differential Emission Measure (DEM) of gradual soft X-ray flares, using the Yohkoh SXT and BCS. The DEM is a measure of how much hot material exists as function of temperature, defined by DEM(T) dT = n² dV, where T is temperature, n is plasma density, and V is volume (Strong et al. 1986). Most studies of BCS data have concentrated on obtaining diagnostics using the good spectral resolution of the BCS in the individual channels. We do not do that. Instead, the BCS is treated as just another run-of-the-mill broad-band detector; all of the line photon flux in each BCS channel is totaled and that data is used in the same way as the SXT data. (The SXT data is, of course, summed over its own spatial resolution.)

For these calculations we use data from the Al.1 (1400 A thick Aluminum), Al12 (12µ thick Aluminum) and Be119 (119µ thick Beryllium) filters of SXT, and the CaXIX and FeXXV channels of BCS. (The SXV channel of BCS is left out because the fits to the DEM are no good when that channel is included; invariably, DEM models which fit the data for the other five filters/channels well--typically to within about 1%--systematically overestimate the SXV photon flux by 50 to 100%. Likewise, we are not including GOES data, models that fit the SXT/BCS data also systematically overestimate the GOES flux.) A plot of the temperature responses for the different channels/filters is shown in fig. 1.

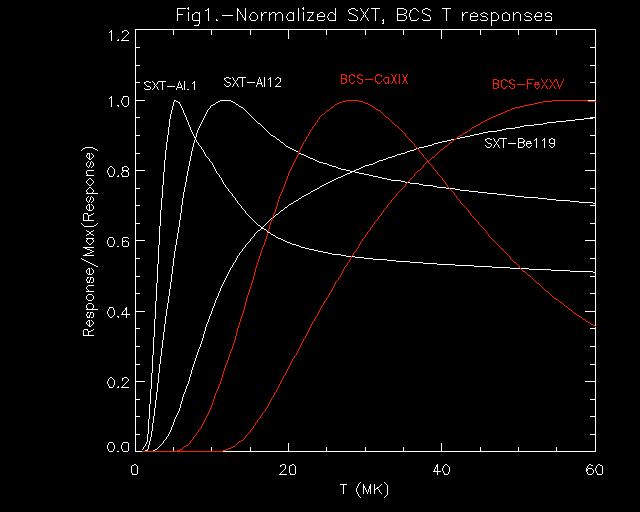
Figure 1. The normalized T response for the SXT filters and BCS channels used. The SXT response curves are white, the BCS responses are in red. Note that the SXT responses extend to high temperatures. Since the T responses are so broad, we do not expect to resolve features in the DEM smaller than a few MK. The BCS responses are obtained using the IDL program BCS_SPEC, which is distributed as part of the SolarSoft software package . The solar coronal abundances used in the SW are adapted from Meyer, J.-P. 1985, Ap. J. Supp. 57, 173.

The analysis was carried out for 92 flares which occurred between October, 1991 and November, 1992. These were chosen from an earlier sample of flares used to obtain the variation of Emission Measure versus Temperature for SXT and GOES, and were chosen so that the peak of emission in each channel/filter was available.

A number of different models for the DEM have been tried, with varying results. Two-temperature models work fairly well for many flares, particularly early in flares. During the flare decays, models for which the DEM is a monotonically decreasing function of temperature often work well. For a number of flares, no model fit the data particularly well; in many of these cases it is obvious that there is a source seen by the BCS, a full-sun instrument, that is not present in the SXT data; in other cases, there are different data gaps for the two different instruments, which are too large for interpolation; for large flares, there may have been saturation problems in the BCS channels; for a few flares, it was clear that there was a high temperature component that was seriously underestimated by the simple DEM models; for some flares there seems to be no reason at all why the data is not fit, these will be dealt with in the future. Note that by ``a good fit'' we mean a reduced chi-squared value of approximately unity, after assuming a systematic error of 5% in the photon flux (poisson errors for the large number of photons involved here are smaller than that). So a ``good fit'' means that the photon fluxes in each channel/filter are within a few percent of the observed data, for the entire flare.

The final sample contains 64 flares.

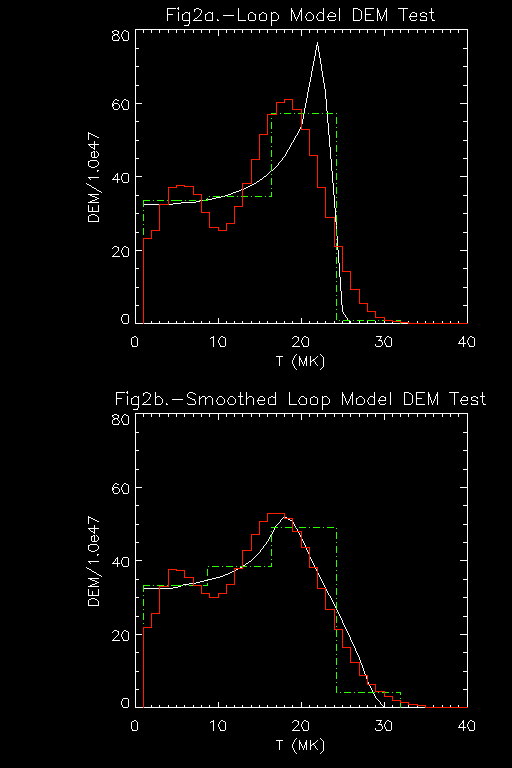
Since both two-component and monotonically decreasing functions seem to fit the data for different flares and time intervals, a model that can show both kinds of behavior is a good thing. We divide the temperature range into 4 bins and assign an emission measure to each bin. The amount of EM in the bins is varied to minimize chi-squared. (We use four bins since we have five data points to work with.) This histogram-DEM usually fits the data fairly well, but we can improve the solution by using it as the starting point for a Maximum Entropy Method (MEM) calculation. (The MEM algorithm is the same as that used for HXT images, see Sakao, 1994.) A sample is shown in fig. 2, in which we compare the fitted DEMs with a flare loop model. Note that the units of all DEMs here will be EM/(10⁴⁷ cm^-3) per MK, so that the total emission measure is the integral of the DEM over T, not ln(T) as is often used.

Figure 2. Top panel, a flare loop model DEM, with fits. The green dot-dash line is a histogram fit to the model, in 4 bins. The red histogram with 1 MK bins is an MEM fit to the data. The true loop model (top panel) has a high-temperature cusp, with a peak at the temperature of the loop apex; MEM does not fit sharp features very well, and it does not fit the the high temperature cusp. In the bottom panel, the high temperature cusp of the input DEM has been smoothed, and the MEM method fits the smooth maximum very well. This is typical for MEM algorithms. The model is a ``static'' loop model of Fisher & Hawley, 1990.

Results

Results for real flares only occasionally look like model results (not truly surprising). DEMs for single-loop limb flares of 13-Jan-92 and 17-Feb-92 are shown in fig. 3 and fig. 4. Loop models typically have a DEM that increases with T, (see fig. 2) and the flares have DEMs that decrease with T. In both cases, there is a distinct high temperature hump in the DEM. This happens for 18 of the 64 flares. When the hump is present, the results look very much like some results obtained from SMM data for a flare of 8-Apr-80 by Strong et al. 1986. The high T component pops up, then increases in emission measure, while decreasing in temperature, until it merges with the low T component. The mean temperature of the low T component remains relatively constant. The behavior is qualitatively similar for the cases which do not show a distinct high T hump. The high T DEM looks like an extended tail on the low T DEM, and it eventually merges with the low T component.

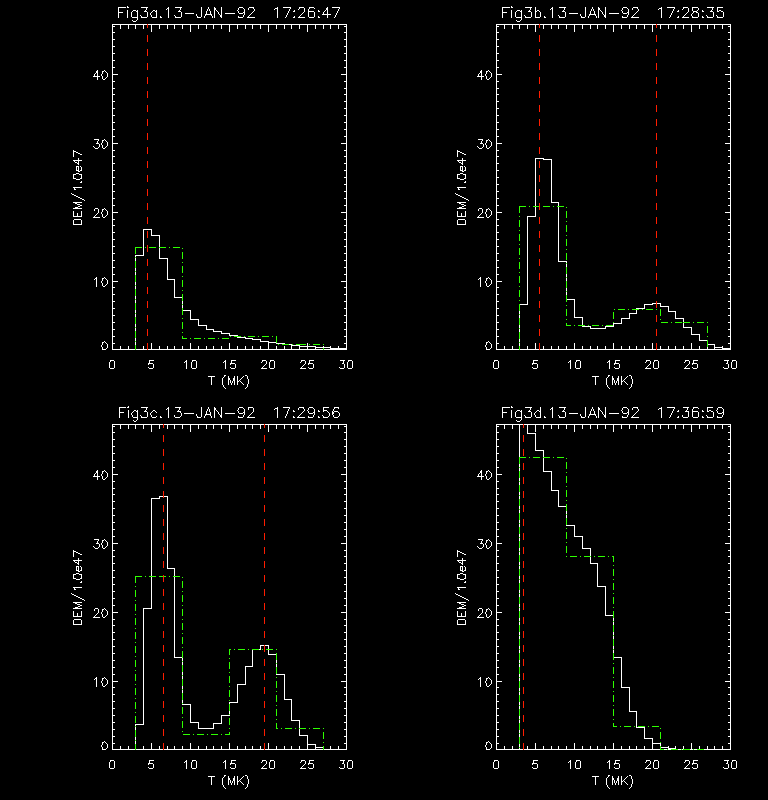
Figure 3. The DEM for different times for the flare of 13-Jan-1992. The green dash-dot line is the histogram-DEM, and the solid line is the MEM-DEM. The values of the temperature for the different components are given by red dashed lines. The four plots correspond to: a) the first SXT Al12 flare-mode image; b) the maximum T for the high T hump; c) the BCS-FeXXV channel maximum; d) the SXT-Al.1 maximum. The high T component is really prominent here. Notice how the peak of the high T component decreases with time as the emission measure increases; the two components merge later in the flare. The temperature of the low T peak does not vary much at all, staying at about 5-6 MK until late in the flare. The results do not look much like loop models, for which the DEM increases with T.

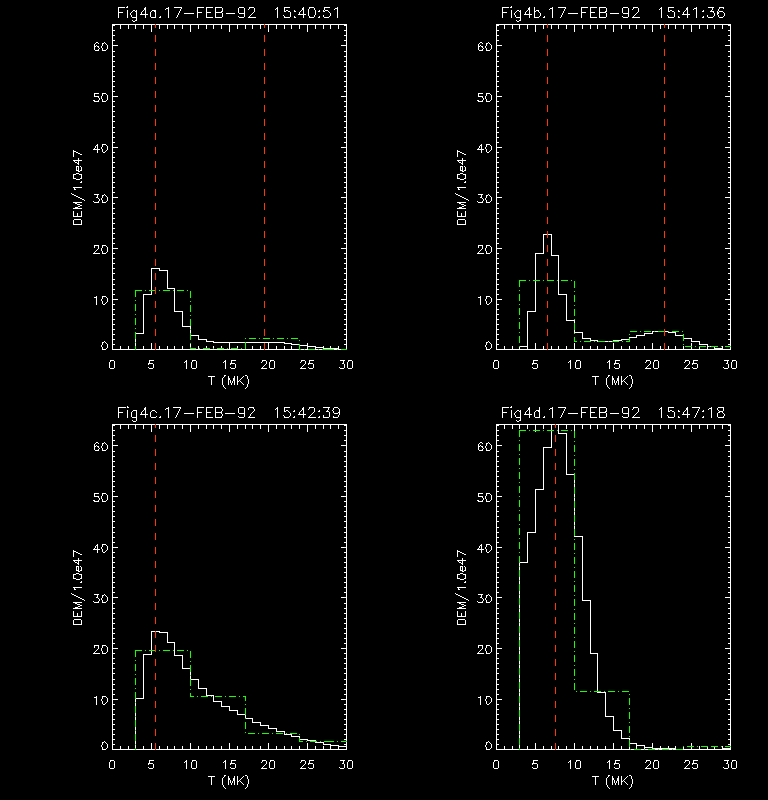
Figure 4. The DEM for different times for the flare of 17-Feb-1992. The format is the same as in fig. 3. Here the high T hump is much less prominent, but the temperature peak (peak T's are denoted by the vertical red dashed lines) is higher, at 22 MK, and there is some DEM above 25 MK. Only 18 out of the 64 flares analyzed showed distinct high T humps, but all flares showed some emission measure in the 20 MK range. The low T component has a relatively high temperature, roughly 6.5-7 MK, as opposed to 5-6 MK for the 13-Jan-92 flare.

Even though the high T component looks small, it can carry a substantial amount of energy. The energy is plotted for the 17-Feb-92 flare in fig. 5, for low and high temperature ranges.

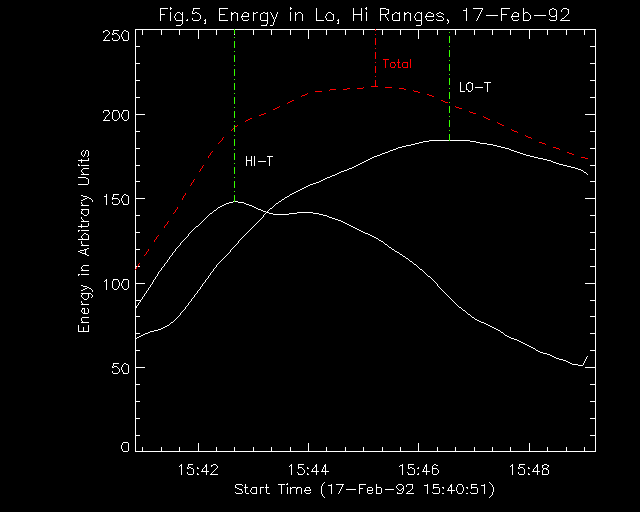
Figure 5. The thermal energy (actually the square root of the integral over dT of T² times the DEM) as a function of time for the 17-Feb-1992 flare. The red dashed line represents the total energy, and the solid lines are for the low and high temperature ranges, arbitrarily divided at 15 MK. Dash-dot vertical lines indicate the peaks for the different components. The energy in the > 15 MK plasma peaks at approximately 15:42:40 (that's right at the end of the hard X-ray impulsive phase, for all of you Neupert Effect buffs), the low T energy peaks a few minutes later, and the total energy, being the sum of the two components, has a peak somewhere in between. Note that all of the energy does not go into the high energy component first. Some, but not all, of the late rise in the low T energy can be attributed to cooling of the high T component, as the two components merge late in the flare. The total energy increases for approximately 2 minutes after the end of the impulsive HXR burst; this may require additional heating beyond that expected from HXR electrons.

The high T stuff peaks earlier, and cools faster. The original motivation for all of this was to see how the plasma cooling time varies as a function of T. For the 17-Feb-92 flare shown in fig.5, the e-folding cooling time is 450 sec for the high T component. The BCS flare-mode observations did not last long enough for us to get a reasonable cooling time for the low T component; we end up using SXT Al.1/Al12 observations, and obtain a cooling time of 500 sec for the low T component. So if the cooling time is proportional to T^q, then a is approximately -0.25. 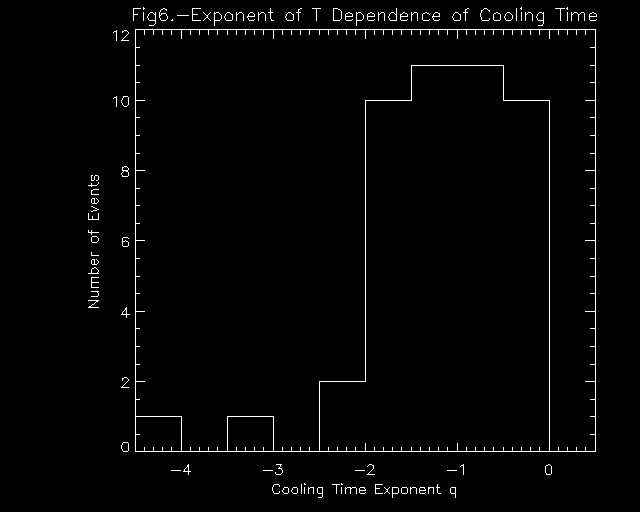For conductive and radiative cooling, q=-2.5 and 1.5 respectively. We found cooling times for 46 of the 64 flares; a histogram or q is shown in fig. 6. We see that q mostly ranges between 0 and -2; this looks more like conductive cooling than radiative cooling, but it could be a combination of the two processes.

Figure 6. A histogram of the exponent, q, of the temperature dependence of the cooling time. We were able to do this calculation for 46 of the flares analyzed. In most cases, SXT Al.1/Al12 data was used to obtain the low T cooling time, since the BCS observations rarely last long enough for us to obtain DEM models for the long times needed for the low T component to lose a significant amount of energy. The values of q vary, but most are in the range between 0 and -2. The negative values of q show that the high T component cools faster than the low T component. This is characteristic of conductive cooling, although the absolute value of q is not as large as is expected from pure conductive cooling, for which q=-2.5

Conclusions

Back to jimm Home page?

Back to Top?

Onwards to the Neupert as a function of T?

Comments to: jimm@ssl.berkeley.edu