How to better determine the power in non-thermal electrons from observed X-ray spectra
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 264 |
| 1st Author: | Eduard Kontar |
| 2nd Author: | Gordon Emslie, Natasha Jeffrey, Nic Bian |
| Published: | 16 November 2015 |
| Next Nugget: | White-light flares |
| Previous Nugget: | Soft and Hard X-rays, Flares, and the Corona |
| List all | |
Introduction
As described in many of these Nuggets, solar flares involve processes that somehow accelerate particles, both electrons and ions, to very high energies. Hard X-rays from solar flares - emitted by the bremsstrahlung process - provide us with the ability to diagnose the nature of the energetic particles responsible for many flare properties. However, an accurate determination of the total number of injected electrons (or, equivalently, their energy content) has challenged modelers for decades. Solar flare hard X-ray spectra in the nonthermal domain typically have power-law forms, which fall steeply with particle energy. Because electrons accelerated in the solar atmosphere will eventually decelerate via collisional losses to ambient partiicles, we often study their emission via the assumption of a thick-target interaction.
Using a cold target model (that retains only the effect of energy loss in the dynamics of emitting electrons) requires that the injected electron flux spectra also decrease rapidly with energy, as in a power law with n(E) ~ E-δ. Hence the total injected energy flux is dominated by the lower limit of the injected energy spectrum. As a result the concept of a “low-energy cutoff” has been used by many authors in order to keep the number and energy content integrals finite. In practice, while fitting the data to a model, for example with OSPEX, we take this cutoff to be the maximum value of the cut-off energy consistent with the hard X-ray data. This establishes lower limits to the number/energy content in the accelerated electrons. This procedure results in an estimate of the minimum (lower bound) energy in the nonthermal electrons. However, a similar upper bound cannot be straightforwardly determined from this approach, so that the overall number/energy content remains highly uncertain.
Warm-cold model
To remedy this situation, one can extend the model to include consideration of a finite temperature of the target (Ref. [1]). This modifies the energy loss rate of the accelerated electrons systematically; such considerations come into play as the electron energies approach a few kT. The reduced energy losses (relative to the cold target results) at low energies make the energy content in the accelerated electrons less sensitive to the assumed low-energy cutoff, to the extent that it can formally be extended down to zero, thus providing an upper bound on the energy content. However Ref. [1] neglected the effects of energy diffusion on the evolution of the energy spectrum, which is critically important at energies of a few kT and is a necessary ingredient for describing the thermalization of the fast electrons in a warm target. Diffusion in both energy and space must be included in a self-consistent analysis of electron transport in a warm target.
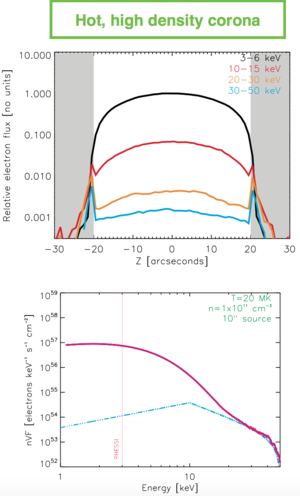
This Nugget follows the analysis of Ref. [2], which highlights the role of thermalization of fast electrons in a model that includes both a warm corona and a cold chromosphere (see Figure 1). The injected/or accelerated electrons first propagate in a coronal plasma that has a temperature comparable to the electron energy, and then collisionally stop in the cold plasma below. The effects of energy loss and diffusion are markedly different in these two regions. Hence, contrary to the case of a purely cold target (in which the spatially-integrated hard X-ray yield is independent of the density profile of the target), in such a composite target the relationship between the hard X-ray flux and the accelerated electron energy content needs to take into account the spatial characteristics of the emitting region, in particular the extent of the warm target region compared to that of the overall flaring region. The resulting mean electron flux spectrum shows a pile-up of thermal electrons (see Figure 2), driven primarily by the effects of energy diffusion in the coronal target. This limits the maximum rate of electron injection and hence provides the much sought-after upper bound on the total injected power.
Summary
Instead of using a cold thick-target model, we advocate the use of the more physically complete warm target model, including the effect of electron thermalization. We have developed a formula that allows explicit determination of this relationship, given the temperature T and extent L of the hot coronal region. A model fit routine f_warm_thick.pro has been developed for the standard RHESSI spectral-fitting softwre OSPEX. This routine allows the determination of the minimum cut-off value and hence the maximum (upper bound) power in non-thermal electrons. For some flares, the low energy cut-off is constrained with an uncertainty of only a couple of keV, providing an accurate estimate of the accelerated electron number/power.
References:
[1] "The Determination of the Total Injected Power in Solar Flare Electrons"
| RHESSI Nugget Date | 16 November 2015 + |
| RHESSI Nugget First Author | Eduard Kontar + |
| RHESSI Nugget Index | 264 + |
| RHESSI Nugget Second Author | Gordon Emslie, Natasha Jeffrey, Nic Bian + |