Fast electrons relaxing
From RHESSI Wiki
(added info box and set date) |
|||
| Line 7: | Line 7: | ||
|publish_date = 2010 August 23 | |publish_date = 2010 August 23 | ||
|next_nugget = The X-ray limb | |next_nugget = The X-ray limb | ||
| - | |previous_nugget = [http://sprg.ssl.berkeley.edu/~tohban/wiki/index.php/Chromospheric | + | |previous_nugget = [http://sprg.ssl.berkeley.edu/~tohban/wiki/index.php/Chromospheric_Plasma_Parameters Chromospheric plasma parameters] |
}} | }} | ||
Revision as of 16:23, 17 August 2010
| Nugget | |
|---|---|
| Number: | 134 |
| 1st Author: | Alec MacKinnon |
| 2nd Author: | |
| Published: | 2010 August 23 |
| Next Nugget: | The X-ray limb |
| Previous Nugget: | Chromospheric plasma parameters |
| List all | |
James Clerk Maxwell
James Clerk Maxwell first wrote down the distribution of velocities in a gas of fixed temperature, a contribution to theoretical physics that most of us now use routinely, without reflection, on a daily basis. The Maxwell-Boltzmann distribution represents a state of maximum entropy, the overwhelmingly most likely state given that the temperature of the gas has been fixed. It is such a standard ingredient of our thinking about gases and plasmas that "non-maxwellian" is one of the trendiest words you can use. A non-maxwellian distribution is of course what we would expect to find in a coronal hard X-ray source, like the one Säm Krucker has described. How would it relax to maxwellian form? Might we recognise this in observations? How efficient is it as a source of hard X-rays? Ross Galloway, Per Helander, John Brown and I have been thinking about this here. I'll describe some of what we've been doing and why it might be interesting for solar hard X-rays. First some more non-maxwellian words.
Kappa distribution
Nonmaxwellian distributions are found ubiquitously in the plasma of the solar wind. They are measured in situ in space and are found to be well described by so-called kappa distributions:
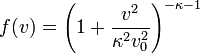
As the parameter 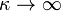 this distribution becomes identical with a Maxwell-Boltzmann, with thermal speed v0. If <math\kappa</math> is small it adds a tail to somethign that looks maxwellain at small speeds.
this distribution becomes identical with a Maxwell-Boltzmann, with thermal speed v0. If <math\kappa</math> is small it adds a tail to somethign that looks maxwellain at small speeds.
We can wave our hands and concoct explanations for the ubiquity of these distributions: there's turbulence, all sorts of microscopic, fluctuating electric fields, a huge range of conditions at its base in the region where it becomes collisionless, it's too tenuous for collisions to re-assert the maxwellian distribution.... This is all very fine and good, but is there a better explanation, something more fundamental, on that we can rely on always to give us kappa distributions?
Possibly!
In fact such an explanation has been suggested, in various forms but possibly with the same key idea at their core. To obtain the Maxwell-Boltzmann distribution we can imagine dividing our velocity space into lots of tiny boxes, dropping electrons one by one randomly into these little boxes, and asking how likely, statistically, a particular distribution across little boxes is. The Maxwell-Boltzmann distribution is the most likely of these possibilities, overwhelmingly so as the number of particles becomes realistically large. But this argument supposes that we really can drop our electrons randomly into the velocity space boxes, independently of what has happened previously. Suppose instead that the probability of an electron being dropped randomly into one velocity space box depends on how many electrons have already been dropped into the neighbouring boxes. Then the Maxwell-Boltzmann distribution would no longer be the most likely. Instead we would find a kappa distribution, like a Maxwell-Boltzmann but with a power-law tail parametrised by a parameter κ. κ parametrises the degree of inter-dependence of velocity space elements and also determines the steepness of the power-law tail. As κ → &infty; we recover the maxwellian form.
| RHESSI Nugget Date | 23 August 2010 + |
| RHESSI Nugget First Author | Alec MacKinnon + |
| RHESSI Nugget Index | 134 + |
