Fast electrons relaxing
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 134 |
| 1st Author: | Alec MacKinnon |
| 2nd Author: | |
| Published: | 2010 August 23 |
| Next Nugget: | The X-ray Limb |
| Previous Nugget: | Chromospheric Plasma Parameters |
| List all | |
Contents |
James Clerk Maxwell
James Clerk Maxwell first wrote down the distribution of velocities in a gas of fixed temperature, a contribution to theoretical physics that most of us now use routinely, without reflection, on a daily basis. The Maxwell-Boltzmann distribution represents a state of maximum entropy, thus the overwhelmingly most likely state given that the temperature of the gas has been fixed. It is such a standard ingredient of our thinking about gases and plasmas that "non-maxwellian" is one of the trendiest words you can use. A non-maxwellian distribution is of course what we would expect to find in a coronal hard X-ray source, like the one described in [1]. How would it relax to maxwellian form? Might we recognise this in observations? How efficient is it as a source of hard X-rays? My colleagues and I have been thinking about this problem [2] and I'll describe some of what we've been doing and why it might be interesting for solar hard X-rays. First some more non-maxwellian words.
Kappa distribution
Non-maxwellian distributions are found ubiquitously in the plasma of the solar wind. They are measured in situ in space. With a total electron density of ne they are found to be well described by so-called kappa distributions:
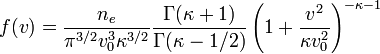
As the parameter 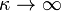 this distribution becomes identical with a Maxwell-Boltzmann, with thermal speed v0. For smaller values of κ the distribution still looks maxwellian at small speeds but displays a 'tail' at high energies (v > v0).
this distribution becomes identical with a Maxwell-Boltzmann, with thermal speed v0. For smaller values of κ the distribution still looks maxwellian at small speeds but displays a 'tail' at high energies (v > v0).
We can wave our hands and concoct explanations for the ubiquity of these distributions: there's turbulence, all sorts of microscopic, fluctuating electric fields, a huge range of conditions at its base in the region where it becomes collisionless, it's too tenuous for collisions to re-assert the maxwellian distribution.... This is all very fine and good, but is there a better explanation, something more fundamental? Possibly.
To obtain the Maxwell-Boltzmann distribution we can imagine dividing our velocity space into lots of tiny boxes, dropping electrons one by one randomly into these little boxes, and asking how likely, statistically, a particular distribution across little boxes is. The Maxwell-Boltzmann distribution is the most likely of these possibilities, overwhelmingly so as the number of particles becomes realistically large. But this argument supposes that we really can drop our electrons randomly into the velocity space boxes and that they are independent of one another. Suppose instead that the probability of an electron being dropped randomly into one velocity space box depends on how many electrons have already been dropped into the neighbouring boxes. Then the Maxwell-Boltzmann distribution would no longer be the most likely. Instead we would find a kappa distribution, where now κ parametrises the degree of inter-dependence of velocity space elements and also determines the steepness of the power-law tail. As 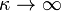 we recover the maxwellian form. Turbulence in a tenuous plasma, for instance, would introduce the necessary correlations in velocity space. This essential idea has of course been put much more elegantly and powerfully, in terms of Tsallis entropy [3] and Gibbsian statistics [4]. Kappa distributions are indicated now by arguments of such generality that we can expect them to result from many electron acceleration scenarios, even if their physical details vary. Jana Kasparova and Marian Karlicky have recently compared the kappa distribution with RHESSI observations [5] and found that it might describe X-ray spectra seen in some coronal sources (which makes sense; we wouldn't expect a single kappa distribution to represent the variety of conditions and transport processes involved in the entirety of a flare).
we recover the maxwellian form. Turbulence in a tenuous plasma, for instance, would introduce the necessary correlations in velocity space. This essential idea has of course been put much more elegantly and powerfully, in terms of Tsallis entropy [3] and Gibbsian statistics [4]. Kappa distributions are indicated now by arguments of such generality that we can expect them to result from many electron acceleration scenarios, even if their physical details vary. Jana Kasparova and Marian Karlicky have recently compared the kappa distribution with RHESSI observations [5] and found that it might describe X-ray spectra seen in some coronal sources (which makes sense; we wouldn't expect a single kappa distribution to represent the variety of conditions and transport processes involved in the entirety of a flare).
Our dream hard X-ray source
Ever since the 1970's solar physicists have looked longingly at 'thermal' hard X-ray sources, in which all the electrons have similar energies. Then collisions between electrons, that make thick target models so inefficient, serve only to redistribute energy and drive the distribution to maxwellian form. In principle the evolution of such a source is mathematically tricky, a diffusion (Fokker-Planck) type of problem in which the diffusion coefficients change all the time, depending on the function we want to know. We found a way of appealing to energy and number conservation that lets us describe most of what is going on without solving this hard numerical problem. We assumed that all our electrons are trapped in a box, given an initial, kappa-like state (not quite kappa but a similar, "core+tail" distribution that lets us do everything analytically) and allowed to evolve by colliding with one another. A sequence of resulting hard X-ray spectra are shown here; these are strongly reminiscent of the evolution of the 'superhot' source discovered in 1980. We estimate that such a source might be 7 - 10 times more efficient at producing hard X-rays than a thick target, i.e. we need 7 - 10 times less energy in electrons to account for a particular, observed hard X-ray flux.
Much of the discussion of such sources around 1980 assumed they would be already relaxed, emitting the exponentially falling X-ray spectrum expected from a maxwellian distribution of electrons. Clever people worried about how to reconcile such a situation with the observed X-ray spectra, that have power-law rather than exponential form. There's no need for this to be the case; all that's necessary is that all electrons have comparable energies, as we suppose here. Until the distribution starts to take on maxwellian form, this source produces a 'nonthermal' X-ray spectrum, like those observed in the the first minutes of a flare.
Also, much of the discussion of these sources at that time focused on the difficulties of bottling up such a source, stopping most of its electrons from just running away, crashing into the chromosphere and simply producing their thick target X-ray yield. The radio and X-ray observations of the 31 December 2007 flare [1] seem to show an effectively contained source, however, whatever the physical mechanism. This could be our dream hard X-ray source!
Not simply our dream hard X-ray source
Energetic electrons contained somehow in the corona should eventually thermalize and produce a 'superhot' X-ray spectrum (i.e. a late phase source consistent with a high temperature maxwellian distribution, as shown in the figure above). Simple energy conservation (alone; without any detailed Fokker-Planck evolution in between) implies a relationship between the value of κ eventually established by the acceleration mechanism (i.e. the power-law slope of the photon spectrum) and the temperature of this eventual superhot source:
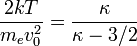
We might hope to test this prediction against data but there's a snag. Säm Krucker emphasises that the 31 December 2007 flare does not develop a superhot component. Neither did the famous, prototype coronal source of the Masuda flare. Our analysis seems not to apply to these sources, but it does at least underline puzzling questions. Does the physical process that accelerates the electrons also trap them in the corona, so that they are no longer contained, to thermalise, once energisation ceases? Or do they rapidly lose energy to some other, non-visible form (maybe plasma waves of some sort)?
Conclusion
We would have wanted to find a way of describing this dream X-ray source even if it doesn't apply in reality; it represents an efficient way of producing hard X-rays, at an opposite physical extreme from the traditional cold, thick target. That it seems not to apply to at least some, observed coronal X-ray sources underlines intriguing questions about the nature of these sources.
As well as my co-authors on the self-interacting electrons paper, I've enjoyed relevant, illuminating discussions with Siming Liu and Säm Krucker on these subjects.
References
[1] Measurements of the Coronal Acceleration Region of a Solar Flare
[3] Fundamental issues on kappa-distributions in space plasmas and interplanetary proton distributions
[4] Gibbsian Theory of Power-Law Distributions
[5] Kappa distribution and hard X-ray emission of solar flares
| RHESSI Nugget Date | 23 August 2010 + |
| RHESSI Nugget First Author | Alec MacKinnon + |
| RHESSI Nugget Index | 134 + |


