The Formation of Kappa Distributions in Solar Flares
From RHESSI Wiki
(initial keyboard entry for 238) |
(Continued keyboard entry) |
||
| Line 20: | Line 20: | ||
In the hard X-ray domain, understanding the particle distribution function - definitely not Maxwellian - has posed substantial theoretical problems. | In the hard X-ray domain, understanding the particle distribution function - definitely not Maxwellian - has posed substantial theoretical problems. | ||
| - | ''RHESSI'' has revealed a new class of hard X-ray sources in which the emission is mainly in coronal loops so dense | + | In statistics, kappa distributions are best known as Student's t-distributions. In the English-language literature this |
| - | that the accelerated electrons are stopped by collisional friction in the corona, rather than streaming through it and impacting on the chromosphere to produce hard X-ray footpoints. Given that the acceleration and HXR emitting regions | + | distribution takes its name from William Sealy Gosset's 1908 paper in Biometrika under the pseudonmym "Student". |
| + | Gossett worked at the Guiness Brewery in Dublin, and was interested in the problems of small samples, for example the | ||
| + | chemical properties of barley. One version of the origin of the pseudonym is that Gosset's employer preferred staff to use | ||
| + | pen names when publishing scientific papers instead of their real name, therefore he used the name "Student" to hide his | ||
| + | identity. Another version is that Guinness did not want their competitors to know that they were using the t-test to test | ||
| + | the quality of raw material. | ||
| + | |||
| + | ''RHESSI'' has revealed a new class of hard X-ray sources in which the emission is mainly in coronal magnetic loops so dense | ||
| + | that the accelerated electrons are stopped by collisional friction in the corona, rather than streaming through it and impacting on the | ||
| + | [http://solarscience.msfc.nasa.gov/chromos.shtml chromosphere] to produce hard X-ray "footpoint sources", so-called because the | ||
| + | hard X-rays illuminate the feet of the coronal magnetic loops. | ||
| + | Flares with HXR footpoints are common, and the new coronal sources have only been discovered recently with RHESSI. | ||
| + | Given that the acceleration and HXR emitting regions appear to be cospatial, these flares are opening new horizons for | ||
| + | the study of acceleration processes ( see Fig.1 ). | ||
| + | |||
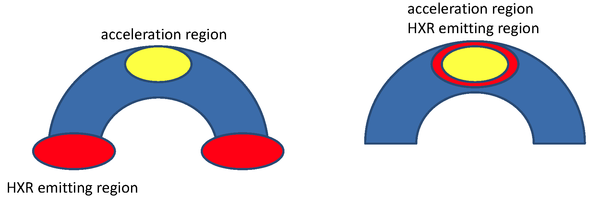
| + | [[File:238f1.png|600px|thumb|center|Fig. 1: | ||
| + | Acceleration (yellow) and HXR (red) emission regions; (left) for | ||
| + | the majority of flares which are dominated by HXR emission in the dense footpoints, (right) | ||
| + | for the type of flares discovered with ''RHESSI'' which are instead | ||
| + | dominated by emission in the dense coronal loop. But recall that with \emph{RHESSI} we only see red not yellow!!! | ||
| + | ]] | ||
| + | |||
| + | In this Nugget, we describe a model for stochastic acceleration in dense coronal loops | ||
| + | where the velocity distribution of HXR emitting electrons is determined | ||
| + | by a balance between acceleration and collisional friction with the dense background | ||
| + | as drawn schematically on Fig.2. | ||
| + | |||
| + | [[File:238f2.png|350px|thumb|center|Fig. 2: | ||
| + | An electron accelerated in a collisional plasma emits HXR's and produces heat by collisional friction with the | ||
| + | background. | ||
| + | Without the acceleration vector pointing downward on this figure, this corresponds to collisional stopping of an HXR emitting electron in a dense background target with the friction force always opposite to the direction | ||
| + | of electron motion. | ||
| + | The situation with the acceleration vector which is random both in amplitude and direction corresponds to ''stochastic acceleration'' of an HXR emitting electron. | ||
| + | ]] | ||
| + | |||
| + | Such a scenario admits a stationary distribution for the electrons that takes the form | ||
| + | of a ''kappa distribution'' with the power-law index κ. | ||
| + | Kappa distributions have a Maxwellian-like core and a power-law tail, and they approach the standard Maxellian distribution when κ becomes large. | ||
| + | as illustrated in Fig. 3. | ||
| + | Kappa distributions are now routinely used as empirical functions for the characterization of particle distribution functions in space plasmas, including electrons in solar flares (see our [http://sprg.ssl.berkeley.edu/~tohban/wiki/index.php/Kappa_Distribution earlier Nugget]. | ||
| + | |||
| + | [[File:238f3.png|350px|thumb|center|Fig. 3: | ||
| + | The kappa distribution f<sub>κ</sub>, for different values of κ. For small values of κ the distribution function has a Maxwellian core and a non-thermal power-law tail. For larger values of κ, the distribution becomes almost indistinguishable from a Maxwellian (from right to left). | ||
| + | ]] | ||
Revision as of 13:44, 10 October 2014
| Nugget | |
|---|---|
| Number: | 238 |
| 1st Author: | Nicolas Bian |
| 2nd Author: | Duncan Stackhouse |
| Published: | October 13, 2014 |
| Next Nugget: | TBD |
| Previous Nugget: | Balmer continuum |
| List all | |
Introduction
A solar flare invariably emits X-rays, and this has almost become its defining property. These X-rays come in two flavors: "hard," above about 10 keV photon energy, marking the non-thermal development of the flare; and "soft," with a well-characterized thermal spectrum including many emission lines. This latter shows thermal physics in the flare, ie with a good match to the expectation from a collisionally-dominated Maxwellian distribution function, consistent with the level populations expected from plasma temperatures in the range 10-20 x 106 K. In the hard X-ray domain, understanding the particle distribution function - definitely not Maxwellian - has posed substantial theoretical problems.
In statistics, kappa distributions are best known as Student's t-distributions. In the English-language literature this distribution takes its name from William Sealy Gosset's 1908 paper in Biometrika under the pseudonmym "Student". Gossett worked at the Guiness Brewery in Dublin, and was interested in the problems of small samples, for example the chemical properties of barley. One version of the origin of the pseudonym is that Gosset's employer preferred staff to use pen names when publishing scientific papers instead of their real name, therefore he used the name "Student" to hide his identity. Another version is that Guinness did not want their competitors to know that they were using the t-test to test the quality of raw material.
RHESSI has revealed a new class of hard X-ray sources in which the emission is mainly in coronal magnetic loops so dense that the accelerated electrons are stopped by collisional friction in the corona, rather than streaming through it and impacting on the chromosphere to produce hard X-ray "footpoint sources", so-called because the hard X-rays illuminate the feet of the coronal magnetic loops. Flares with HXR footpoints are common, and the new coronal sources have only been discovered recently with RHESSI. Given that the acceleration and HXR emitting regions appear to be cospatial, these flares are opening new horizons for the study of acceleration processes ( see Fig.1 ).
In this Nugget, we describe a model for stochastic acceleration in dense coronal loops where the velocity distribution of HXR emitting electrons is determined by a balance between acceleration and collisional friction with the dense background as drawn schematically on Fig.2.

Such a scenario admits a stationary distribution for the electrons that takes the form of a kappa distribution with the power-law index κ. Kappa distributions have a Maxwellian-like core and a power-law tail, and they approach the standard Maxellian distribution when κ becomes large. as illustrated in Fig. 3. Kappa distributions are now routinely used as empirical functions for the characterization of particle distribution functions in space plasmas, including electrons in solar flares (see our earlier Nugget.
| RHESSI Nugget Date | 13 October 2014 + |
| RHESSI Nugget First Author | Nicolas Bian + |
| RHESSI Nugget Index | 238 + |
| RHESSI Nugget Second Author | Duncan Stackhouse + |
