Dense Loop Flares
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 181 |
| 1st Author: | Jingnan Guo |
| 2nd Author: | Gordon Emslie |
| Published: | 6 August 2012 |
| Next Nugget: | RHESSI Catches Gamma-Ray Bursts |
| Previous Nugget: | The Slowest Flare |
| List all | |
Contents |
Introduction
For decades, there has been much discussion of flare models in which copious non-thermal electrons are accelerated in a reconnecting current sheet in the solar corona. In such models the electron transport and bremsstrahlung processes are decoupled from the acceleration site. However, recently we have found a group of flares showing extended coronal sources which seem to combine the processes of electron acceleration, propagation and energy loss due to Coulomb collisions (see reference [1] and papers cited there). We have found that the observed variation of loop length with photon/electron energy is consistent with a collisional propagation model, but with an extended acceleration region embedded within it. Best fits to such a model allow us to obtain estimates for the plasma density in, and the longitudinal extent (parallel to the field) of, the acceleration region. These quantities in turn allow us to determine the number of particles within the acceleration region and the filling factor ‘f’: the ratio of the emitting volume to the volume that encompasses the emitting region(s). Knowing both the number of particles in the acceleration region and the rate of acceleration of particles above a certain reference energy (obtained from spatially-integrated hard X-ray data) also allows inference of the specific acceleration rate (electrons accelerated per second per ambient electron, units s-1), a measure of the efficiency of the acceleration process. These results have implications both for the global electrodynamics associated with the replenishment of the acceleration region and for the nature of the particle acceleration process.
Mathematical Tools
From the primary RHESSI modulation patterns, we construct images and maps of the mean electron flux, a weighted distribution of the radiating particles. This involves processing the observationally-deduced photon and electron visibilities respectively (Fig. 1 gives the scheme for this). Several image-processing methods can be used to analyze RHESSI data: a visibility-based ForWarD-fit (FWD) algorithm, a maximum entropy (MEM) procedure, and the UV-Smooth (UVS) approach described in a previous Nugget. For the flares selected for study here, all three methods reveal the flare structures as elongated loops, but we focus on the results obtained with the UVS algorithm. We have found this to be very accurate when reconstructing relatively localized extended sources as considered here.

Nonthermal Collisional Model
Let F(E, s) denote the electron flux spectrum at longitudinal position s, measured from the assumed center of the acceleration region near the loop top.
Various physical processes, especially Coulomb collisions with ambient electrons, can in principle contribute to the behavior of F. If the electron acceleration occurs principally near the loop top (s=0), resulting in the injection of energetic electrons with a power-law distribution (spectral index δ) into a target with uniform density n, then the form of F(E,s) can be deduced from the continuity and energy loss equations as:
![]()
The longitudinal extent of the source external to the acceleration region can be found by considering the standard deviation:
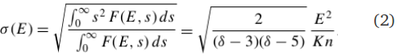
Now let’s extend this model to include the acceleration of electrons within a finite region extending from s=−L0/2 to s= L0/2. Neglecting energy losses in the acceleration region, this assumption can be relaxed, but this causes only relatively minor changes to the results.
The longitudinal source extent L(E) is then given by:
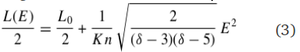
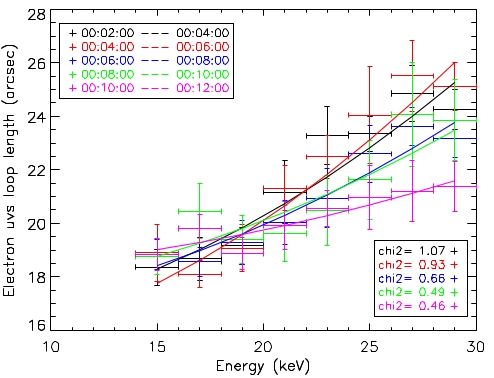
A similar expression can be derived for the variation of source length with photon energy L(e). The above equation can be easily understood: higher energy electrons are able to propagate further from the acceleration region and hence produce hard X-ray emission over a greater spatial extent than lower-energy electrons. For each flare, the values of the acceleration-region length and the loop density are obtained by best-fitting the above equation to the form of L(E) obtained from the UVS maps directly in the electron domain. Fitting results of one of the selected flares are shown in Figure 2. The source lengths for each time interval are well-fit by a quadratic form.
Results and Interpretations
The above analysis technique has been applied to 22 coronal loop events observed by RHESSI (reference [1]). For each event, the values of the acceleration region size (length L0 , width W and volume V0), loop density n, the number of particles inside the acceleration region N , the specific acceleration rate η (for electrons above 20 keV) and the filling factor f are deduced from the model, as shown in Table 1. We have also calculated the value of the (geometric) mean value of each quantity over the ensemble of events.
The mean value of the filling factor obtained is consistent, within a logarithmic standard deviation or so, with unity. This validates the common assumption that most of the observed flare volume contains emitting plasma. The observationally-deduced value of the specific acceleration rate (~0.01 per second) implies that all available electrons would be energized and ejected toward the footpoints within a few hundred seconds. This result has significant implications for the supply of electrons to the acceleration region, current closure, and the global electrodynamic environment in which electron acceleration and propagation occur (see reference [2]). The value of the specific acceleration rate for Event 4 is consistent with that determined independently by Gabriele Torre (Genova), who used a continuity equation analysis of the variation of the electron flux spectrum throughout the source. This systematic result, for an entire class of events, appears to represent a significant constraint on theoretical models for particle acceleration in flares.
References
[1] Properties of the Acceleration Regions in Several Loop-structured Solar Flares
| RHESSI Nugget Date | 6 August 2012 + |
| RHESSI Nugget First Author | Jingnan Guo + |
| RHESSI Nugget Index | 181 + |
| RHESSI Nugget Second Author | Gordon Emslie + |