On the Correlation of HXR and WL Emission in Solar Flares
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 265 |
| 1st Author: | Matej Kuhar |
| 2nd Author: | |
| Published: | 23 November 2015 |
| Next Nugget: | Hard X-ray stereoscopy with MiSolFA |
| Previous Nugget: | Better estimation of electron fluxes |
| List all | |
Contents |
Introduction (Or, what do we know so far?)
In a solar flare, the energy is emitted over the whole electromagnetic spectrum; particularly interesting is the radiation in the "white light" (WL) range, because it contains such a significant fraction of the total flare energy. Even though the first detection of a solar flare was done by Carrington and by Hodgson (as long ago as 1859) in WL, observations in this wavelength range are difficult due to the relatively faint enhancement of WL emission due to the flare, compared to the non-flaring, pre-flare level. It was due to this reason that WL flares were long considered to be rare and exotic phenomena; however, with the development of new observatories, WL emission has been detected in weaker flares (even GOES C-class flares). Numerous studies have explored the correlation of hard X-ray (HXR) and WL emission in solar flares, observed to be both in space and in time. There are two mechanisms proposed for explaining this correlation: 1) direct heating, in which the precipitating electrons from the corona locally heat and ionize the middle chromosphere, after which a WL continuum emission is produced directly by the recombination of hydrogen, and 2) radiative back-warming, in which electrons are stopped in the upper chromosphere. In the latter scenario, the recombination produces UV continuum radiation that irradiates the photosphere below, resulting in enhanced continuum emission from the photosphere itself. The two models predict different heights for WL/HXR sources and, equally important, their formation from the same (direct-heating) or different volumes (radiative back-warming) in the solar atmosphere. In this Nugget, we will present the results of a statistical study on the correlation of HXR and WL emission in solar flares. We identified 43 white-light flares (WLFs) for this study, spanning GOES classes M and X, as observed by the HMI instrument on the SDO observatory spacecraft.
Observations and data analysis
Observations were made using RHESSI and HMI for the HXR and WL range, respectively. From RHESSI data, we had the information about the timing and positions of the flares. This was used to guide the HMI search. For each flare, we overlaid RHESSI and HMI images and calculated the WL flux of the part of the active region that lay inside the 30% contour of RHESSI emission. We calculated the time evolution of WL emission for a long interval around the time of the flare. This gave us lightcurves such as those presented in Figure 1. In this figure we can see the WL lightcurves for two extreme examples from the sample, an X2.1 flare and an M2.4 flare. When we plot the WL lightcurves on the same scale, we can see how faint the WL signal in the latter event really is. From these lightcurves, we chose the peak- and pre-flare frames, made background-subtracted images in WL, and calculated the WL flux inside the 30% RHESSI contour. The HXR fluxes were calculated by fitting a composite spectrum with thermal (soft X-ray) and power-law (hard X-ray tail) to the RHESSI data. The energy deposition by non-thermal electrons was derived from the HXR spectral parameters, using the thick-target approximation.

Results
In Figure 2, we can see a relation between WL fluxes and HXR fluxes at 30 keV on the right, and between WL fluxes and HXR spectral indices on the left. We can see that there exists a clear correlation between the two fluxes, with the correlation coefficient (between logarithmic values of fluxes) of about 0.7. The correlation is not linear, but a power law with an index of (0.61 +- 0.07). The absence of a linear correlation is not surprising, as the conversion of HXR flux and WL flux at the HMI wavelength to the actual energy input and output does not need to be linear. There is no correlation between WL fluxes and HXR spectral indices. This result suggests that the highest energy electrons play a minor role in the production of WL emission, which is reasonable from an energetical point of view as the low-energy electrons carry more energy than the high-energy electrons (due to their larger numbers).
The correlations presented above are with the directly observed quantities. In the ideal case, we would like to compare the total energy input by non-thermal electrons to the energy output (i.e. radiative losses in the optical range). These estimates rely heavily on model assumptions. To calculate the total energy input, we use the standard thick target model. The calculation of total energy output in WL range is more difficult since we only have single-frequency observations. Therefore, in this case we stick with WL fluxes in the comparison to the total energy input. The correlation between the two quantities is presented in Figure 3, for the total deposited power by non-thermal electrons above 50 keV. Again, the relation is not linear, but a power law with the index of about 0.6.
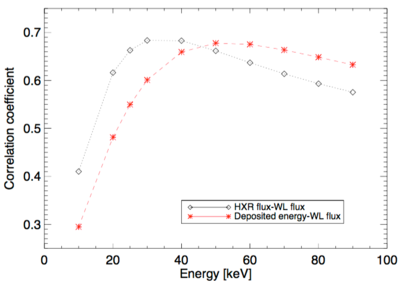
In Figure 4, we show the behavior of the correlation coefficient between WL fluxes and power deposited by non-thermal electrons above different cut-off energies in one case, and between WL fluxes and HXR photon fluxes at different energies in the other case. Both show a steep decrease for energies below 30 keV and a gradual decrease towards higher energies. This behavior can be explained within the standard thick-target model as the lowest energy electrons are stopped too high in the solar atmosphere to be responsible for WL production. The highest energy electrons, on the other hand, do not carry enough energy to account for the overall WL emission. We can also notice a shift between the two curves: the peak is at 30 keV for the flux-flux correlation coefficient, and at 50 keV for the power-flux correlation coefficient. This difference is a direct result of the thick-target assumption; electrons of a given energy produce photons of all lower energies.
Where do we stand now?
From the results of this statistical study, we conclude that WL and HXR fluxes show a clear correspondence in space, time, and intensity. The best correlation is achieved for electrons of energies of about 50 keV. If the HXR and WL sources are indeed co-spatial as recent studies suggest, we propose the following scenario for the WL formation. The 50 keV electrons produce the WL emission by directly heating dense layers by collisions to moderate temperatures (of order 10^4 K). The lower-energy electrons lose their energy above the WL/HXR source at lower densities producing hot plasma (around 107 K), which radiates at EUV and SXR wavelengths. The WL source dissipates part of the flare energy that was stored in the high-energy tail of accelerated electrons through radiative cooling, while the energy in the low-energy electrons goes into heating of the plasma, part of which then evaporates and produces the main flare loop.
An open question which remains is the observation of low altitudes of WL/HXR sources in recent studies. This observation is challenging to explain within the standard thick-target model, as it would require strongly beamed electron distribution and/or very low density of the flaring atmosphere. Our results point towards the moderate-energy electrons as having a major role in producing WL emission; however, it does not give conclusive answer on the formation heights.
Acknowledgments
This Nugget derives from Ref. [1], with co-authors Säm Krucker, Juan Carlos Martínez Oliveros, Marina Battaglia, Lucia Kleint, Diego Casadei, and Hugh Hudson
References
[1] "Correlation of Hard X-ray and White Light Emission in Solar Flares", to be published in ApJ, 2016.
| RHESSI Nugget Date | 23 November 2015 + |
| RHESSI Nugget First Author | Matej Kuhar + |
| RHESSI Nugget Index | 265 + |

