A Global Survey of EUV Coronal Power Spectra
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 367 |
| 1st Author: | Karl Battams |
| 2nd Author: | |
| Published: | 31 December 2019 |
| Next Nugget: | John Brown |
| Previous Nugget: | Cosmic Rays over the Rainbow Bridge |
| List all | |
Contents |
Introduction
We observe solar flares and CMEs by image sequences, an example of time-domain astronomy carried out with multi-wavelength images sequences (movies) for the most part. For each pixel in an individual movie frame, a characterization of the nature of the variability produces a spectrum somewhat analogous to its wavelength spectrum, for instance via its power spectrum. In principle, one could ask, why would the entire vast volume of the SDO image database not be pipeline-processed to reveal this information?
Analysis of power spectra obtained from solar observations has long been a subject of interest, yielding valuable information about turbulent and oscillatory processes throughout all regions of the solar atmosphere. Such studies were bolstered by the advent of missions such as TRACE, which could returnd high spatial and temporal resolution that enable the derivation of high-quality power spectra over small spatial regions.
Here we outline a Python-based computational pipeline that efficiently reduces tens of gigabytes of SDO data into a series of massively reduced data parameterizations based upon the power-spectral properties of the observations.
Processing Pipeline
Our processing pipeline can be summarized as follows: Obtain primary data → Define region of interest (up to 2000x2000 pixels tested) → derotate observations → extract intensity time series → convert to power spectra → fit models → create parameterizations.
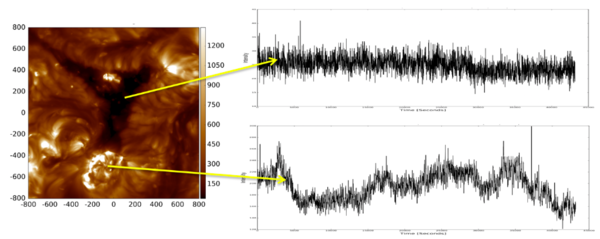
Extracting power spectra from SDO observations first requires the extraction of intensity time series (light curves) from individual pixels in some given region of interest (ROI). This step requires the solar observations first be "de-rotated" to account for the differential rotation of the solar atmosphere, before pixels in a user-defined region of interest are extracted into a datacube of dimensions [x,y,t]. Our technique allows for datacubes of up to approximately [2000px,2000px,12hrs] at SDOs full cadence (12s).
Figure 1 shows examples of typical intensity time series extracted from individual pixels in a 1600x1600px 12-hr data cube: the top time series represents a pixel in a coronal hole, and the bottom a pixel in the umbra of a sunspot. Here both are in the 193Â passband, though the technique works equally welll for the 193Â 284Â, 171Â, 304Â, 1600Â and 1700Â passbands as well. Each x,y element of the datacube then yields a power spectrum via Fourier transformation.
Inspection of these power spectra reveals unique aspects that relate to the features from which they are extracted. For example, a coronal hole yields a steep slope (turbulence) following a power law, whereas the sunspot shows the expected oscillation in the 3-5-minute region, superimposed upon a background power law.
Model Fitting
Broadly speaking, the power spectra of all different solar features (coronal holes, filaments, active regions, etc) have unique spectral properties that relate to the underlying physics in those regions. To better understand these processes, a pioneering study (Ref. [1]) showed power spectra over small spatial regions of the corona and found that they could generally be described by a simple power law plus a Gaussian spectral excess. The power-law captures the overall sloping behavior of the spectrum, relating to convective turbulence and the energy transfer within that region, and a Gaussian to characterize the dominant oscillatory process, if any. We have built upon this work by replacing the Gaussian component with a Lorentzian, in order to improve the characterization of damped oscillations (which we assume to be occurring within certain regions of the corona).
For each power spectrum [P] in the data cube (1.6-million power spectra in a 1600x1600px region), we fit two models, a simple power-law model, M1:
and a power-law-plus-Lorentzian model, M2:
with an amplitude coefficient [A], power-law index [n], and the tail coefficient [C] in the simple P1 model, and the additional Lorentzian amplitude [α], location [β] and width [δ]. Our code compares the residuals of the fits to both models and makes a decision as to which model best fits each unique spectrum. Figure 2 shows examples of two complete model fits to two different power spectra corresponding to a bright loop foot point (c) and sunspot umbra (d).
Results
Our technique enables the production of (beautiful!) visualizations of our model parameters that show full images of the fit parameters (power law index, Lorentzian location and FWHM of the Lorentzian) for a 1600x1600px region of AIA 193Â, Figure 4) and 304Â (Figure 5) over a 12-hour period. This region contained numerous loops, a large coronal hole, and a small sunspot (approx. pixel location [0,-400]).
Optimization
Performing model fits to well over a million individual power spectra is computationally intense, taking up to several days in a naive single-process pipeline. Our code takes advantage of the relative ease of multi-processor implementation in Python to distribute the spectral fitting over as many processing cores as are available. Testing on up to 20 processing cores reduced the entire pipeline (data extraction, de-rotation, FFT transform, and model fitting) to less than four hours for the analysis of a 1600x1600x12hr data cube.
Summary
Our "imaging power spectroscopy" modeling work (Ref. [2]) presents a methodology that can reduce a massive (tens of Gb) data set into a handful of visualizations that capture and describe some of the unique physical processes occurring at all levels of the corona. In testing, we have found it would be feasible to run our process continuously on realtime SDO observations over a sliding window, producing such parameter maps several times per day. Our method would also be applicable to any data set for which stable intensity time series could be obtained. It may also prove useful for observatories such as DKIST, whose vast data volumes will benefit enormously from pipeline-styule reduction/synopsis techniques.
References
[1] "Coronal Fourier Power Spectra: Implications for Coronal Seismology and Coronal Heating"
[2] "A Global Survey of EUV Coronal Power Spectra"
| RHESSI Nugget Date | 31 December 2019 + |
| RHESSI Nugget First Author | Karl Battams + |
| RHESSI Nugget Index | 367 + |