Empirical Constructs and Cartoons
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 222 |
| 1st Author: | Forrest Mozer |
| 2nd Author: | Hugh Hudson |
| Published: | March 24, 2014 |
| Next Nugget: | Homing in on Flare Energy |
| Previous Nugget: | Imaging Quasi-Periodic Oscillations in a Simple Flare |
| List all | |
Contents |
Introduction
When we work with data to try and learn something about the nature of the Universe, space scientists and astronomers often find gaps in their knowledge. This is not such a problem in laboratory physics, where one has more direct control of the machinery. Accordingly we resort to working models and try to tie our observations to them. At the most basic level we have the "empirical construct": a simple concept with a name and therefore an implied referent. An empirical construct is a model, etc. that exists in your mind but not in the physical world. At a more complex level, we can have a "cartoon" which might embrace several empirical constructs. A cartoon is like a graphical interpolation formula that - under optimal conditions - allows us to link one observation to another in a form of prediction.
We need cartoons to understand how to link different observations of solar flares into a working model, even if it is very approximate.
The basic building block is the empirical construct, and this Nugget discusses the conditions under which a given emprical construct makes sense physically. To give away the answer, we believe that it is a good one if independent observers can agree upon its nature. In other words, can it be measured unambiguously? The world of MHD offers great examples of both good and bad empirical constructs, and we describe a couple of them below. The archive of solar flare cartoons offers a much wider variety of improbable empirical constructs, and sometimes it seems as though the further you go from Earth, the greater the density of failed empirical constructs.
A good MHD empirical construct
The magnetic field line in a static plasma configuration seems to be a good empirical construct. It has no physical reality, and yet any observer armed with a good enough compass can track the field from point A to point B better tham an electron with a large enough Larmor radius. In this sense, one can generate a measurement, concluding that yes, two points do fall on the same field line, plus an error bar on the measurement, and everybody can be happy. This is true even if Maxwell's equations do not need magnetic field lines to work properly.
The empirical construct of "field line" is therefore useful because there is almost no circumstance in which one is led to an incorrect physical conclusion from thinking about magnetic field lines - in a static configuration.
A bad MHD empirical construct
The idea of a moving magnetic field line actually contradicts Maxwell's equations directly, and is therefore a bad empirical construct (see Ref. [1]). This can be shown analytically, which we do next, and also is clear from numerical simulations. If at an initial time a field line (good construct) leads from point a to point b. If the plasma moves with velocity E x B, one can readily show that this implies
B x (∇ x E‖) = 0
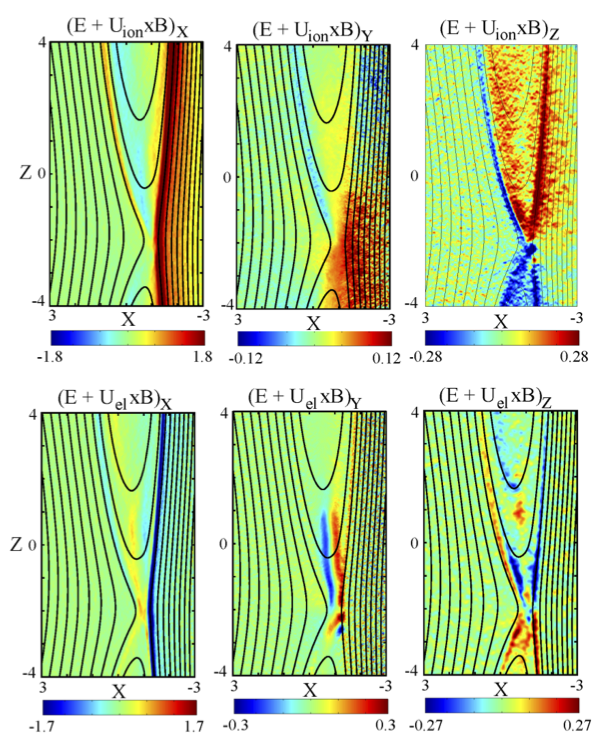
and to determine B as a function of time, one needs to solve Maxwell's equations in any case for which there is a finite E‖. The 3D PIC simulation shown in Figure 1 illustrates the development of B x (∇ x E‖) via PIC simulations of asymmetric magnetic reconnection at the Earth's magnetopause.
Cartoons
There are many more empirical constructs, some useful, some not, and some downright misleading. We have had a distinguished committee review the two we've described above, and they produced the report in Figure 2.
On beyond these basic concepts there are the cartoons, some of which try to put lots of these empirical constructs together into a package that represents a global situation. For example, the standard CSHKP flare cartoon contains moving field lines, shock waves of several sorts, line tying, magnetic loop, thermal conduction, magnetic reconnection, and particle acceleration. Figure 3 shows a rich example.

Many of these constructs warrant closer inspection if not downright skepticism. The cartoonist really cannot avoid this wholesale simplification of the physics, though, because the observations are both hugely detailed and yet at the same time terribly incomplete - that's the astronomer's dilemma.
Conclusions
As we go further afield from the basement laboratory, we often find ourselves at a loss for physical direct confirmatory evidence of a physical process that all can agree upon. Experiments become unrepeatable and morph into "observations" instead. Our sound instinct in this case is to work with a construct we know to be "real" in the sense that two experimenters can in fact check each other's work, and we have noted that the magnetic field line in a static configuration is not very controversial in this sense. A moving field line, on the other hand, raises substantial questions in any interesting dynamic plasma, specifically one that involves magnetic reconnection, and indeed we have been warned long ago not to use this concept. Nevertheless many people do rest their thinking on such a construct, and the world of solar flare cartoons provides any number of examples.
Usually imagining a field line to be moving through space sounds consistent with the frozen-in field concept, but we must recall that Alfvén himself - the inventor of the concept - repudiated it as long ago as 1976, claiming it to have been a great mistake. Anybody who is sketching scientific cartoons understands that they are meant not to be taken literally, and must be supplanted as the field evolves. In that sense any cartoon that outlives its usefulness actually may impede progress, in the sense that observers diligently try to identify the properties the cartoon has invoked, even to the exclusion of noticing interesting new things! We should all be a bit careful.
References
[1] "Motion of magnetic lines of force"
| RHESSI Nugget Date | 24 March 2014 + |
| RHESSI Nugget First Author | Forrest Mozer + |
| RHESSI Nugget Index | 222 + |
| RHESSI Nugget Second Author | Hugh Hudson + |
