The X-ray Limb
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 135 |
| 1st Author: | Hugh Hudson |
| 2nd Author: | Gordon Hurford |
| Published: | 2010 September 6 |
| Next Nugget: | Quiet Sun III |
| Previous Nugget: | Fast electrons relaxing |
| List all | |
Contents |
Introduction
The radius of the Sun, 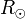 , certainly is one of the most important basic pieces of astrophysical information.
But how does one know it?
Obviously the edge of a solar image (its limb) is pretty well defined, but sound basic physics tells us that it is fuzzy on the scale of about 0.01%.
For a mean radius of 969.63'' as obtained from the world-standard "Allen's Astrophysical Quantitites" [1] there is a claimed error bar of about 30 ppm (parts per million, thus 0.003%).
Do we really know the solar radius that well?
How could we, in fact?
In measuring
, certainly is one of the most important basic pieces of astrophysical information.
But how does one know it?
Obviously the edge of a solar image (its limb) is pretty well defined, but sound basic physics tells us that it is fuzzy on the scale of about 0.01%.
For a mean radius of 969.63'' as obtained from the world-standard "Allen's Astrophysical Quantitites" [1] there is a claimed error bar of about 30 ppm (parts per million, thus 0.003%).
Do we really know the solar radius that well?
How could we, in fact?
In measuring 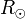 we imagine a fictitious solar atmosphere, one characterized by a stable layered structure comprising features such as the photosphere, chromosphere, and transition region.
This is really not so correct because the solar atmosphere is full of spectacular blemishes, as noted early on by Galileo and others.
we imagine a fictitious solar atmosphere, one characterized by a stable layered structure comprising features such as the photosphere, chromosphere, and transition region.
This is really not so correct because the solar atmosphere is full of spectacular blemishes, as noted early on by Galileo and others.
The significance of the actual number (why do we need to know it so precisely?) lies, for example, in the arcane discipline of helioseismology. Here we find exceedingly precise measurements of the fundamental modes of oscillation of the body of the Sun; sound waves essentially can be trapped in the interior and reverberate for long periods of time. The solar tones can be purer than those of a pitch pipe or a tuning fork!
The traditional radius measurement
The precise location of the limb of the Sun depends upon the wavelength of observation. At a given wavelength there will be an absorption coefficient for the emitted photons, which via Kirchhoff's radiation law and the assumption of thermal equilibrium will correspond to the emission coefficient. For standard visible continuum, the main absorption is the interaction of between a free electron and a neutral hydrogen atom. The astronomer's name for this is [H-] radiation because there is in fact a stable bound atomic state of the system of one proton and two two electrons. There is [H-] free-bound emission into this state, and [H-] free-free emission if the second electron simply swings close to an ordinary neutral hydrogen atom. Although this process is dominant and can be calculated accurately, there are still major uncertainties in the opacity as a function of height and hence the location of the limb. These uncertainties reflect other contributions to the opacity as well as hydrodynamics and plasma physics, which regulate the ionization state of the medium and its vertical extent. The uncertainty is hinted at by any white-light picture of the Sun, which readily shows the surface granulation. This convective motion, and other dynamical effects, result in ubiquitous flows and three-dimensional spatial structures that average together to form the limb. All of these uncertainties normally get wrapped up into a complicated numerical model - a "semi-empirical atmosphere" that mimics the observed spectrum but which does not describe the physics well.
A better idea: hard X-rays
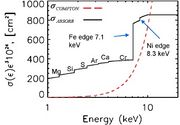
The better idea is simply to use hard X-ray absorption to determine the height distribution of the mass. RHESSI is the first hard X-ray imager with sufficient angular resolution to do this. While the X-ray absoprtion depends on modeling as well, it does so much more weakly. The opacity above about 10 keV (see Figure 1, provided by Eduard Kontar and Natasha Jeffrey (see their recent Nugget) depends solely on Compton scattering by electrons. This is exactly the same situation as for the ordinary white-light corona, which shines entirely by scattered light. There are subtle complexities and so modeling still is necessary, but to a much lesser extent.
Occulted sources
To locate the limb by X-ray absorption, one must have an occulted source. Ideally one could use [cosmic X-ray sources], which are numerous and which have negligible angular extent. This each occultation or de-occultation by the solar limb of a background quasar (or whatever) should make it possibly to measure R_sun at the point of contact. Unfortunately, most of these sources are too faint. It is not so clear that one could not do a statistical study anyway, in which many sources each contributed a little signal in a [http://sprg.ssl.berkeley.edu/~tohban/wiki/index.php/Chree_Analysis_for_Flares summed-epoch analysis]. But the easiest thing to do first is just to make use of flares that happen to occur on the far side of the Sun. There are many of these and they can be extremely bright.
RHESSI is well set up to make this measurement because of its unique modulation optics. These make it possible to study visibility phases, an excellent way to locate the limb in an absolute sense if one has sufficiently good metrology. In its absence one can still do relative radius measurements, comparing one flare to another, to study time variations and latitude dependence (oblateness) for example.
Figure 2 shows the precision requirement. The height of optical depth unity is a sensible limb definition. The Figure shows where it occurs as a function of height as referred to the standard radius value (ref. [1]). The three curves are for two X-ray energies just above and below the iron K edge at 7.1 keV (see Figure 1), and the other (red) is for a higher energy where only Compton scattering matters. The angular separation of the limb location at the different X-ray energies is small, but within RHESSI's reach.
Conclusion
We have described a fundamentally new way to determine a fundamental astronomical quantity, R_sun. It will require a great deal of effort to achieve success, and so this first public announcement is a kind of recruiting poster - contact the authors please if you are interested! Otherwise stay tuned to these Nuggets and in a couple of years we will hope to have some results anyway.
References
[1] Allen's astrophysical quantities
| RHESSI Nugget Date | 6 September 2010 + |
| RHESSI Nugget First Author | Hugh Hudson + |
| RHESSI Nugget Index | 135 + |
| RHESSI Nugget Second Author | Gordon Hurford + |