Chromospheric Plasma Parameters
From RHESSI Wiki
| Nugget | |
|---|---|
| Number: | 133 |
| 1st Author: | Stephanie Chow |
| 2nd Author: | Hugh Hudson |
| Published: | 2010 August 2 |
| Next Nugget: | Fast electrons relaxing |
| Previous Nugget: | Harmonic Oscillations |
| List all | |
Contents |
Introduction
Most of the electromagnetic emission of a solar flare appears to originate in the chromosphere, and indeed all of the mass elevated into the corona must originally come from this layer of the solar atmosphere as well. Thus we really need to understand the plasma physics of this region. From the RHESSI point of view, for example the hard X-ray footpoint sources probably are mainly in the chromosphere and involve complicated plasma physics there. Unfortunately our astronomical observations of the chromosphere are fleeting and incomplete - without instrumentation, the chromosphere only appears to the human eye during a total eclipse. So, to understand the plasma physics we must rely upon numerical models. In this Nugget we describe Web pages that provide some information about the values of typical plasma-physics parameters in the solar chromosphere.
The definitions of many plasma parameters can be found via Wikipedia or the NRL Plasma Formulary. Our Web pages (ref. [1]) have applied these definitions to a set of model chromospheres derived by Juan Fontenla and collaborators (ref. [2]). In this Nugget, we introduce the parameters and show some height dependences using three of the models tabulated by Fontenla. These models were chosen to represent a range in physical conditions from the quiet sun to the sunspot umbra; the original motivation for constructing the models was to help in partitioning the solar disk into physically distinct zones that have markedly different radiation spectra and thus contribute in different was to the total solar irradiance variations.
Models, Plots & Data
Fontenla himself has published work on his models and plasma parameters derived from them, but our website provides this kind of information as a general tool for public access. The three models we used correspond with the quiet sun, bright faculae, and the umbra of a sunspot. These cover the most extreme range within the full array of models. For example, the gas pressure at the top of each model marks the point at which the temperature jumps up suddenly between the chromosphere and corona. The transition region pressures for our three cases are 0.2, 2, and 4 dynes/cm2, respectively.
The home page contains links to the Fontenla models we used, plots of parameters from the models, and derived parameters we calculated. Each link will take the user to a page comprised of a brief description of the parameter, the equation used to derive it, and a plot that shows the parameter plotted against height (e.g.Figure 1).
Visitors can also obtain the Fontenla model data we used and the data produced from the calculations by downloading the .txt files. To make things as user-friendly as possible, we also included a downloadable reader that will take the .txt files and read them in IDL. (Note: the downloadable readers on each page are different, but have essentially the same skeletal structure. The only differences will be which parameter is included and how many variables are provided.)
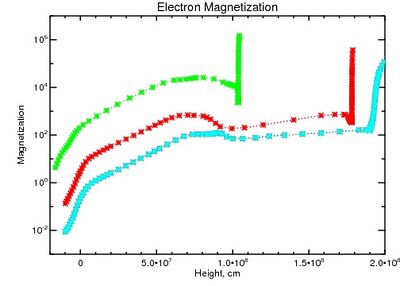
The example parameter shown in Figure 1 is the electron magnetization, defined as the ratio of electron gyrofrequency to the electron collision frequency. If the magnetic field is relatively strong, the electrons are "magnetized" - the gyrofrequency is directly proportional to the magnitude of B. In an unmagnetized plasma, ie with the value of magnetization below about unity, many collisions happen in each gyration of the electron around the field, which therefore becomes less important in guiding it.
The plot shows that the magnetization increases with height, and becomes quite large at the highest altitudes. We generally believe that electrons in the solar corona are indeed fully magnetized, which readily accounts for the striations that one sees in eclipse images. The reason for this increased magnetization is of course simply that the density falls off faster than B, so that collisions lose their dominance.
Limitations
The basic Fontenla models derive from the theory of [radiative transfer] and attempt basically to fit a mean model of the vertical structure in order to make the emitted spectrum match as well as possible. This is the approach known as the semi-empirical model atmosphere. This kind of model simply omits much of the physics that would interest a plasma physicist: small-scale structure, including turbulence; 3D structure; shock waves; particle distribution functions (requiring the electron and proton temperatures to be equal eliminates large amounts of physics!) etc. Thus the parameters we estimate on this basis have limited quantitative accuracy.
Conclusions
We have introduced a set of Web pages that display and make available estimates of parameters useful for studying the plasma physics of the chromosphere of the Sun. There are very likely to be errors at the time of this Nugget, but we hope to eliminate these with the help of feedback from readers. We also would appreciate hearing about problems with the user interface, since we would like for these pages to be generally useful. Finally we would also like to hear about any forthcoming applications of plasma physics to the solution of the many outstanding problems in understanding how the solar chromosphere actually works.
References
[1] Chromospheric Plasma Parameters
| RHESSI Nugget Date | 2 August 2010 + |
| RHESSI Nugget First Author | Stephanie Chow + |
| RHESSI Nugget Index | 133 + |
| RHESSI Nugget Second Author | Hugh Hudson + |